For the following circuit, determine ix using the Superposition Theorem:
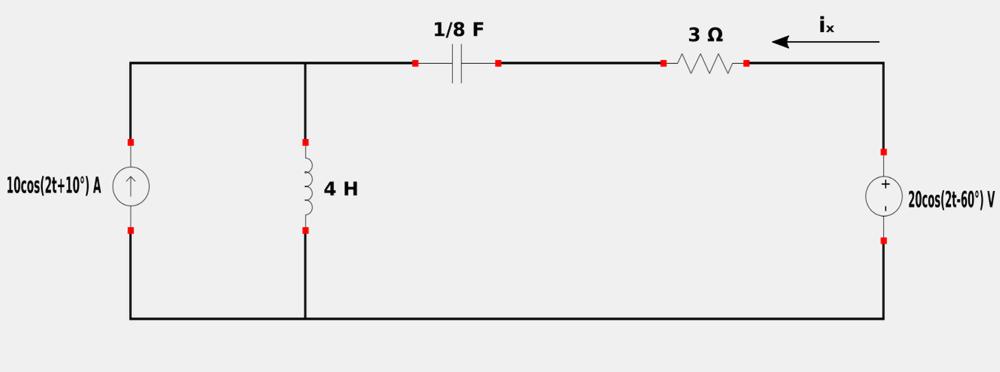
Recall the steps taken to analyze a circuit using the Superposition Theorem:
- "Turn off" all independent sources except one source. Determine the output voltage/current due to the remaining source.
- Repeat step #1 for each remaining independent source.
- Find the total contribution by adding all of the individual contributions from each independent source.
Our strategy will involve finding the value of ix due solely to the voltage source and then finding the value of ix due solely to the current source. Each individual contribution will then be summed together to get a value for ix as depicted in the above circuit. Start by letting:
$$ i_1 = i_x \; due \; to \; current \; source. $$ $$ i_2 = i_x \; due \; to \; voltage \; source. $$
Step 1: Determine i1 ("turn off" voltage source):
With the current source acting alone, the angular frequency (omega) is 2. This allows us to obtain the following impedance values for the inductor and capacitor: $$ \mathbb{Z}_L = j\omega L = j(2)(4) = j8 \; \Omega $$ $$ \mathbb{Z}_C = \frac{-j}{\omega C} = \frac{-j}{2(\frac{1}{8})} = -j4 \; \Omega $$ We then transform the current source to the frequency/phasor domain: $$ 10\cos(2t+10^{\circ}) = 10 \angle 10^{\circ} $$ With the voltage source "turned off" and everything transformed to the frequency domain, the circuit looks like the following:
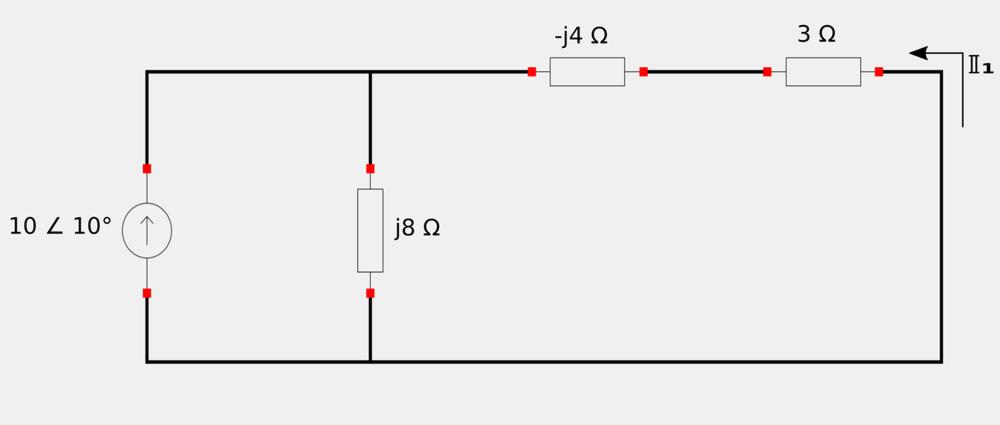
...which can be further reduced to the following circuit:
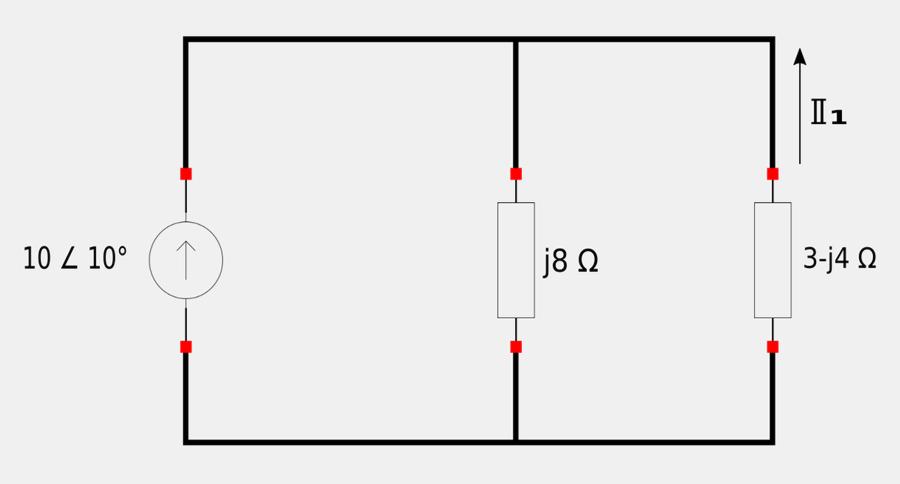
Using the principle of current division with the above circuit and keeping in mind the sign convention with respect to the labeled arrows in the schematic we get: $$ -\mathbb{I}_1 = \Big( \frac{j8}{3-j4+j8} \Big) 10 \angle 10^{\circ} $$ $$ = \Big( \frac{j8}{3+j4} \Big) 10 \angle 10^{\circ} $$ Converting the fraction to phasor form: $$ -\mathbb{I}_1 = \Big( \frac{8 \angle 90^{\circ}}{5 \angle 53.13^{\circ}} \Big) 10 \angle 10^{\circ} $$ $$ -\mathbb{I}_1 = 16 \angle 46.87^{\circ} $$
$$ \mathbb{I}_1 = 16 \angle 226.9^{\circ} $$
In the previous page it was mentioned that individual responses must be converted to the time-domain prior to being added if the independent sources are operating at different frequencies. Here in our case however, the voltage and current sources are both operating at the same frequency. Thus we can leave i1 and i2 in the phasor/frequency domain and add them. If this were not the case you would proceed to multiply the above-determined value for i1 (currently in phasor form) by the frequency factor (e^jwt) and take the real part of the result in order to get its time-domain representation.
Step 2: Determine i2 ("turn off" current source):
With the voltage source acting alone, the angular frequency (omega) is also 2. Therefor, the impedance values will be the same as we calculated in step #1. Converting the voltage source to the frequency domain gives us: $$ 20\cos(2t-60^{\circ}) = 20 \angle (-60^{\circ}) $$ So with the current source "turned off" and everything converted to the frequency domain we have the following circuit:
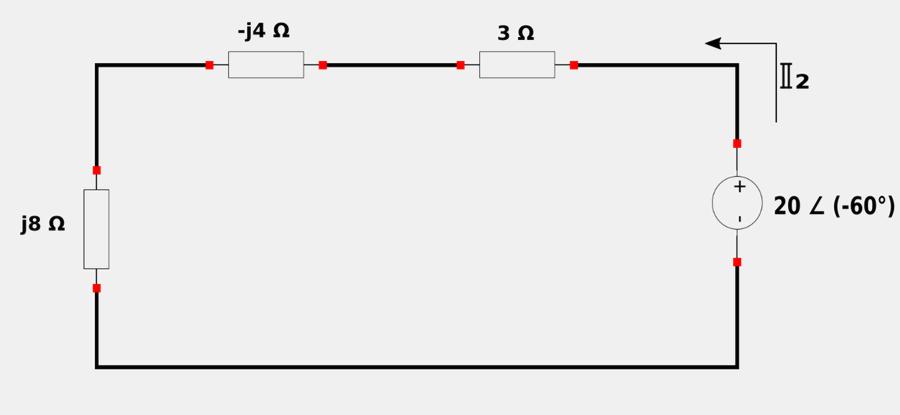
Using Ohm's Law for the above circuit gives us: $$ \mathbb{I}_2 = \frac{20 \angle (-60^{\circ})}{\mathbb{Z}_{eq}} $$ $$ \mathbb{I}_2 = \frac{20 \angle (-60^{\circ})}{3-j4+j8} $$ $$ \mathbb{I}_2 = \frac{20 \angle (-60^{\circ})}{3+j4} $$ $$ \mathbb{I}_2 = \frac{20 \angle (-60^{\circ})}{5 \angle 53.13^{\circ}} $$
$$ \mathbb{I}_2 = 4 \angle (-113.1^{\circ}) $$
Step 3: Determine total response by summing individual responses:
As per the Superposition Theorem, the current through the 3 ohm resistor (ix) is the sum of the current through that same resistor due to each independent source acting alone (i1 and i2). Therefore: $$ \mathbb{I}_x = \mathbb{I}_1 + \mathbb{I}_2 $$ Remember that in this case, we can add phasors since omega (angular frequency) is the same for both independent sources. $$ \mathbb{I}_x = 16 \angle 226.9^{\circ} + 4 \angle (-113.1^{\circ}) $$ Converting to rectangular form: $$ \mathbb{I}_x = -10.93 - j11.68 - 1.569 - j3.679 $$ $$ \mathbb{I}_x = -12.5 - j15.36 $$ ...and back to phasor form: $$ \mathbb{I}_x = 19.8 \angle 230.9^{\circ} $$ If we convert the above expression from polar to exponential notation we get:
$$ \mathbb{I}_x = 19.8e^{j230.9^{\circ}} \qquad,(Eqn \; 1) $$
Transform the total response from the frequency domain to the time domain:
In order to do this we multiply equation #1 by the frequency factor (e^jwt) and take the real part of the result (as explained in the tutorial on Phasor Notation.) In our case here, omega is equal to 2. $$ i_x = R_e \{ 19.8e^{j230.9^{\circ}} e^{j2t} \} $$ $$ i_x = R_e \{ 19.8e^{j(2t+230.9^{\circ})} \} \qquad,(Eqn \; 2)$$
Recall Euhler's Identity: $$ e^{j\theta} = \cos\theta + j\sin\theta $$ ...and apply it to equation #2:
$$ i_x = R_e \{ 19.8\cos(2t+230.9^{\circ}) + j19.8\sin(2t+230.9^{\circ}) $$ By evaluating the above expression we arrive at our final answer:
$$ i_x = 19.8\cos(2t+230.9^{\circ}) $$
Let's take a look at another example:
Continue on to Superposition Theorem example 2
