Determine the transfer function for the following circuit:
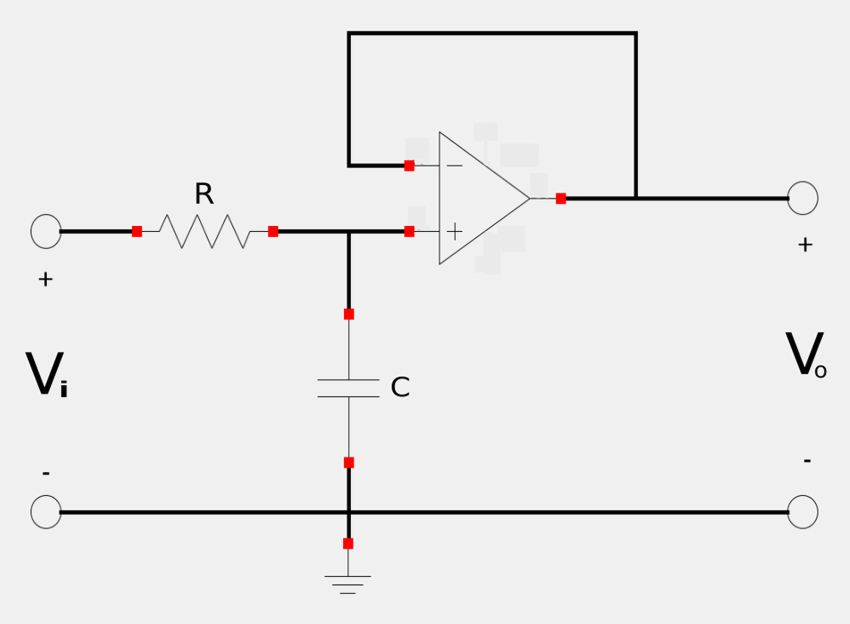
Recall that the transfer function in terms of voltage gain is defined as: $$ \mathbb{H}(\omega) = \frac{\mathbb{V}_o(\omega)}{\mathbb{V}_i(\omega)} $$ We begin by determining the voltage present on the non-inverting terminal of the op-amp. By the principle of voltage division we have: $$ \mathbb{V}_+ = \frac{\mathbb{Z}_C}{\mathbb{Z}_R+\mathbb{Z}_C} \; \mathbb{V}_i $$ $$ \quad = \frac{\frac{1}{j\omega C}}{R+\frac{1}{j\omega C}} \; \mathbb{V}_i $$ $$ \quad = \frac{\frac{1}{j\omega C}}{\frac{jR\omega C+1}{j\omega C}} \; \mathbb{V}_i $$ $$ \mathbb{V}_+ = \frac{1}{1+jR\omega C} \; \mathbb{V}_i \qquad,(Eqn\;1) $$ Recall that the first rule for ideal op-amps states that: $$ \mathbb{V}_+ = \mathbb{V}_- $$ We also notice that for our circuit: $$ \mathbb{V}_- = \mathbb{V}_o $$ Therefore: $$ \mathbb{V}_+ = \mathbb{V}_- = \mathbb{V}_o $$ Equation #1 no becomes: $$ \mathbb{V}_o = \frac{1}{1+jR\omega C} \; \mathbb{V}_i $$ By rearranging terms, we arrive at the transfer function for the circuit:
$$ \frac{\mathbb{V}_o}{\mathbb{V}_i} = \frac{1}{1+jR\omega C} = \mathbb{H}_{\omega} $$
Continue on to active filter example problem #2...
