The following active filter has a cutoff frequency of 1 kHz as well as a 120 mV variable frequency source.
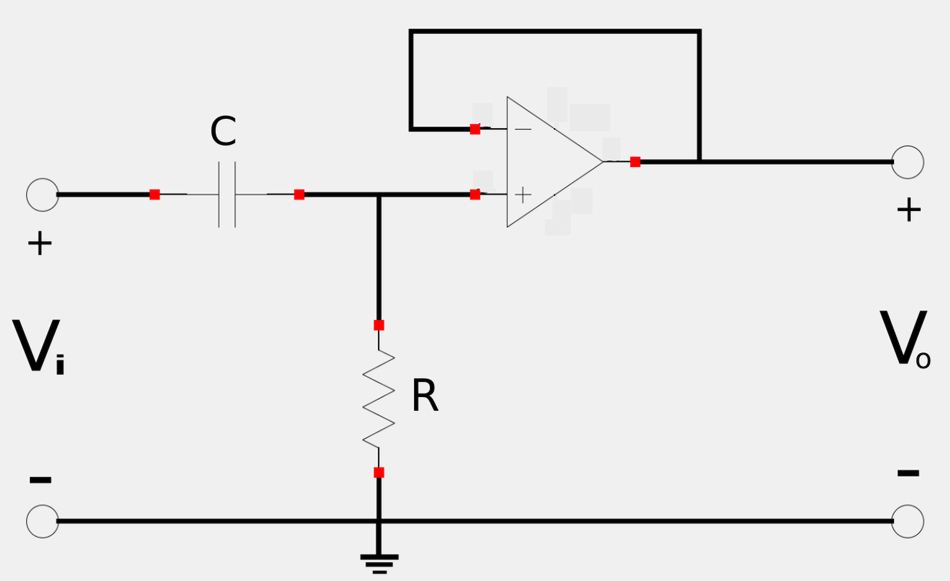
Determine the output voltage at:
- A) 200 Hz
- B) 2 kHz
- C) 10 kHz
Determine an expression for output voltage:
Recall that according to the rules for ideal op-amps: $$ \mathbb{V}_+ = \mathbb{V}_- $$ For our circuit notice that: $$ \mathbb{V}_- = \mathbb{V}_o $$ Therefore: $$ \mathbb{V}_+ = \mathbb{V}_o $$ By using the principle of voltage division we have: $$ \mathbb{V}_+ = \frac{\mathbb{Z}_R}{\mathbb{Z}_C+\mathbb{Z}_R} \; \mathbb{V}_i = \mathbb{V}_o $$ $$ \mathbb{V}_o = \frac{R}{\frac{1}{j\omega C}+R} \; \mathbb{V}_i $$ $$ \mathbb{V}_o = \frac{R}{\frac{1+j\omega C}{j\omega C}} \; \mathbb{V}_i $$ $$ \mathbb{V}_o = \frac{R}{\frac{1}{j\omega C}+R} \; \mathbb{V}_i $$
$$ \mathbb{V}_o = \frac{1}{1-\frac{j}{RC\omega}} \; \mathbb{V}_i \qquad,(Eqn\;1) $$
Express the output voltage in terms of the cutoff frequency:
In this example problem we are given a single cutoff frequency. This means that the filter must be either a high-pass or low-pass design. For either filter, the cutoff frequency is defined as: $$ \omega_C = \frac{1}{RC} $$ This means that we can rewrite equation #1 as: $$ \mathbb{V}_o = \frac{1}{1-\frac{j\omega_C}{\omega}} \; \mathbb{V}_i \qquad,(Eqn\;2) $$ Additionally, note that we are given the corner frequency in terms of hertz and to convert to radians per second we have the following expression: $$ \omega_C = 2\pi f_c = 1000 $$ $$ \omega_C =2000\pi $$ We can now rewrite equation #2 as: $$ \mathbb{V}_o = \frac{1}{1-\frac{j2000\pi}{\omega}} \; \mathbb{V}_i \qquad,(Eqn\;3)$$
Determine an expression for the magnitude of the output voltage:
This is done by taking the magnitude of equation #3: $$ |\mathbb{V}_o| = \mathbb{V}_i \Big[ \frac{1}{\sqrt{1+(\frac{2000\pi}{\omega})^2}} \Big] \qquad,(Eqn\;4) $$
Determine the output voltage for each input frequency:
Plug each of the input frequencies into equation #4:
A) f=200 Hz
$$ \omega = 2\pi(200) = 400\pi \frac{rad}{sec} $$ $$ |\mathbb{V}_o| = (120\times 10^{-3}) \Big[ \frac{1}{\sqrt{1+(\frac{2000\pi}{400\pi})^2}} \Big] $$
$$ |\mathbb{V}_o| = 23.53\;mV $$
B) f=2 kHz
$$ \omega = 2\pi(2000) = 4000\pi \frac{rad}{sec} $$ $$ |\mathbb{V}_o| = (120\times 10^{-3}) \Big[ \frac{1}{\sqrt{1+(\frac{2000\pi}{4000\pi})^2}} \Big] $$
$$ |\mathbb{V}_o| = 107.3\;mV $$
C) f=10 kHz
$$ \omega = 2\pi(10,000) = 20,000\pi \frac{rad}{sec} $$ $$ |\mathbb{V}_o| = (120\times 10^{-3}) \Big[ \frac{1}{\sqrt{1+(\frac{2000\pi}{20,000\pi})^2}} \Big] $$
$$ |\mathbb{V}_o| = 119.4\;mV $$
