Determine i(t) and v(t) for the following circuit:

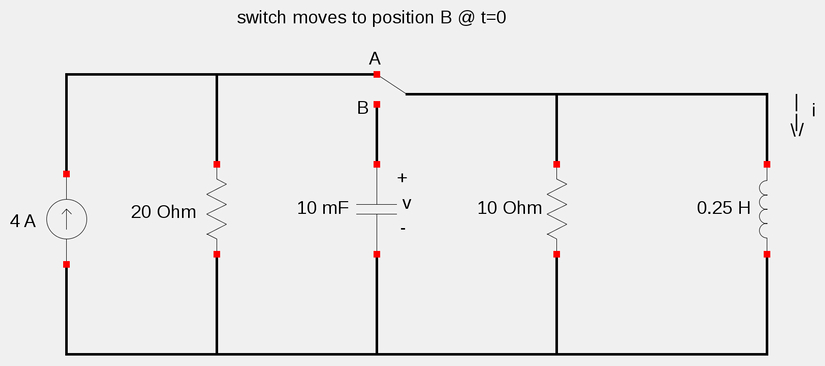
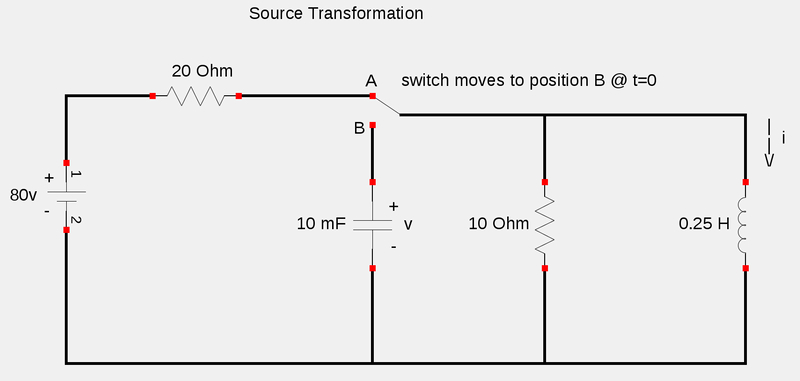
Let's first use our knowledge of Norton/Thevenin equivalent circuits to perform a source transformation and replace the current source that is in parallel with the 20 ohm resistor with a voltage source in series with the same resistor. The resulting equivalent circuit is shown below:

The following circuit is at a time t<0, where the switch has been in position A for a long enough time to assume steady state conditions. Recall that under steady state conditions an inductor acts as a short circuit and a capacitor acts as an open circuit.

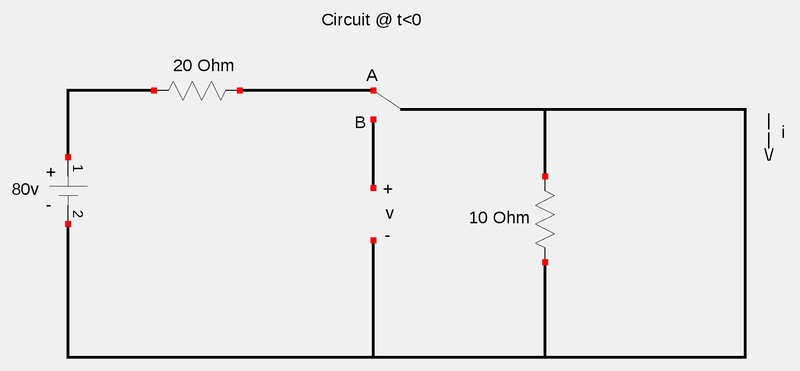
Determining initial condition i(0)

In the above circuit, we realize that no current will flow through the 10 ohm resistor. When considering the outer loop of the circuit (and using Ohm's Law), i(0) is:

$$i(0) = \frac{80 \; v}{20 \; \Omega} = 4 \; A$$

Furthermore, when using Kirchoff's Voltage Law around the left-most loop in the circuit, we obtain the following:

$$20i(0) + v(0) - 80 =0 $$

$$20(4) + v(0) = 80 $$

$$v(0) = 0 \; v $$

Lastly, we will determine a numerical value for v'(0) by examining the circuit shown below which is for times t>=0.

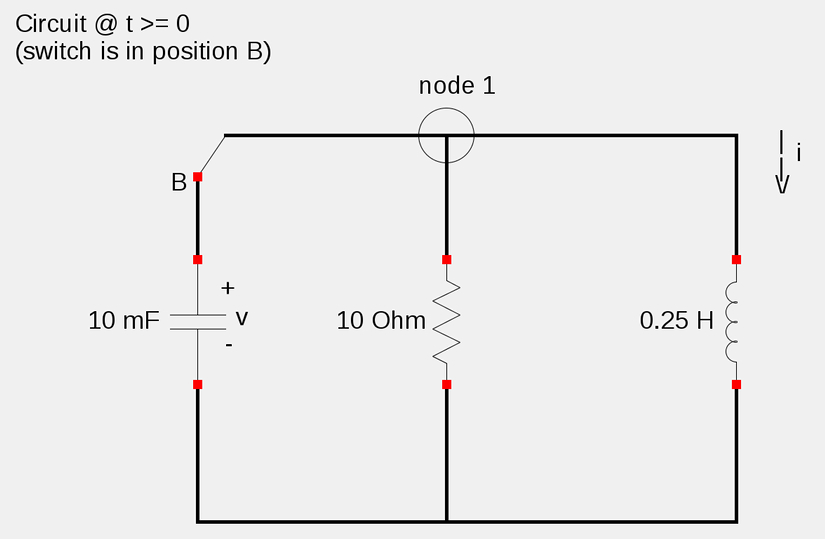
Using Kirchoff's Current Law (KCL) at node one gives us the following equation

$$Cv'(0) + \frac{v(0)}{R} + i(0) = 0 $$

$$10(10^{-3})v'(0) + \frac{0}{10} + 4 = 0 $$

Solving for v'(0) gives you:

$$v'(0) = -400 \frac{v}{s} $$

We have now determined numerical values for the following initial conditions:

Initial Conditions:

$$v(0) = 0\;v $$

$$v'(0) = -400 \frac{v}{s} $$

$$i(0) = 4 \; A $$

Next we will obtain a 2nd order differential equation for the natural response of our circuit at t>=0

Once again we use KCL at node 1 in the above circuit as well as the following three expressions for the current through our resistor, inductor and capacitor:

$$I_R = \frac{V}{R} $$

$$I_L = \frac{1}{L} \int_{}^{} v \; dt $$

$$I_C = C \frac{dv}{dt} $$

Doing so gives us the following expression at node 1:

$$Cv' + \frac{v}{R} + \frac{1}{L}\int_{}^{}v \;dt = 0 $$

...and if we take the derivative of the above expression, we get:

$$Cv'' + \frac{1}{R}v' + \frac{1}{L}v = 0 $$

We now divide through by C:

$$v'' + \frac{1}{RC}v' + \frac{1}{LC}v = 0 $$

...and plug in our values for R, L and C:

$$v'' + \frac{1}{10(10mF)}v' + \frac{1}{0.25(10mF)}v = 0 $$

$$v'' + 10v' + 400v = 0 \qquad (Eqn \; 1) $$

Equation #1 is a 2nd order homogeneous differential equation and just as in the previous page, we will use a substitution that assumes v(t) and its 1st/2nd derivatives to be of the following form:

$$v = e^{st} $$

$$v' = se^{st} $$

$$v'' = s^2e^{st} $$

If we substitute the above three expressions into equation #1, we get:

$$s^2e^{st} + 10se^{st} + 400e^{st} = 0 $$

Dividing through by the exponential term gives us:

$$s^2 + 10s + 400 = 0 \qquad (Eqn \; 2) $$

Equation #2 is our "characteristic equation". In order to find the roots of the characteristic equation we will use the quadratic formula:

$$s = \frac{-b \pm \sqrt[]{b^2-4ac}}{2a} \qquad ,(Quadratic \;formula)$$

By proceeding to do so, we obtain the following complex roots:

$$s_{1,2} = -5 \pm j5 \sqrt{15} $$

$$s_{1,2} = -5 \pm j19.36 $$

$$s_1 = -5 + j19.36 $$

$$s_2 = -5 - j19.36 $$

...where:

$$j = \sqrt{-1} $$

Taking only root s1 and plugging it into our substituted expression for v(t):

$$v(t) = e^{s_1t} $$

$$v(t) = e^{t(-5+j19.36)} $$

$$v(t) = e^{-5t}e^{tj19.36} $$

Now recall Euhler's Identity:

$$e^{j \theta} = cos(\theta) + jsin(\theta)$$

...and apply it to the exponential term with the imaginary "j" in the exponent:

$$v(t) = e^{-5t}[cos(19.36t) + jsin(19.36t)] $$

we then disregard the imaginary "j" which gives us:

$$v(t) = e^{-5t}cos(19.36t) + e^{-5t}sin(19.36t) $$

We also recognize that the above expression represents a fundamental set of solutions to equation #1:

$$v(t) = \{e^{-5t}cos(19.36t) \;,\; e^{-5t}sin(19.36t) \} $$

Also, given a solution to a 2nd order homogeneous differential equation, multiplying that solution by a constant also results in a solution. Additionally, given two unique solutions to such an equation means that the sum of those two solutions is also a solution. All of this means that v(t) can be represented by:

$$v(t) = Ae^{-5t}cos(19.36t) + Be^{-5t}sin(19.36t) \qquad(Eqn \; 3) $$

Equation #3 represents the "general solution" to our original differential equation (equation #1)

We will now proceed use our previously-determined initial conditions to solve for the constants (A,B) of equation #3

Initial Conditions:

$$v(0) = 0\;v $$

$$v'(0) = -400 \frac{v}{s} $$

$$i(0) = 4 \; A $$

$$v(0) = Ae^{-5(0)}cos[19.36(0)] + Be^{-5(0)}sin[19.36(0)] = 0$$

$$A = 0 $$

Now determine the derivative of equation #3:

$$v'(t) = -19.36Ae^{-5t}sin(19.36t) - 5Ae^{-5t}cos(19.36t) $$

$$ \qquad \qquad + 19.36Be^{-5t}cos(19.36t) - 5Be^{-5t}sin(19.36t)$$

...therefor:

$$v'(0) = -5A + 19.36B = -400 $$

$$-5(0) + 19.36B = -400 $$

$$B = -20.67 $$

By plugging our newfound values for constants A and B into equation #3 we obtain the following expression for v(t) (which is the natural response of the voltage across the capacitor for all times 0s and greater.)

Voltage across capacitor (final answer)

$$v(t) = -20.67e^{-5t}sin(19.36t) \qquad for \; t \geq 0 $$

Determining current through the inductor, i(t)

In order to find i(t), we will use the following definition for current through an inductor:

$$i_L = \frac{1}{L} \int_{}^{} v \; dt + i(0)$$

$$i_L = \frac{1}{0.25}(-20.67) \int_{}^{} e^{-5t}sin(19.36t) \; dt + 4$$

$$i_L = -82.68 \int_{}^{} e^{-5t}sin(19.36t) \; dt + 4$$

Evaluating this integral will require the implementation of Integration by Parts (IBP). I won't explain the implementation here, but feel free to check out my Integration by Parts Tutorial where I evaluate this exact integral. After evaluating the integral we have:

$$i_L = -82.68[-0.0125e^{-5t}sin(19.36t) - 0.0484e^{-5t}cos(19.36t)] + 4 + C $$

...where C is our constant of integration

After distributing the -82.68 we get:

$$i_L = 1.034e^{-5t}sin(19.36t) + 4e^{-5t}cos(19.36t) + 4 + C \qquad (Eqn \; 4)$$

We will now solve for our constant of integration (C) by using our previously determined numerical value for i(0). (i(0) = 4)

$$i(0) = 1.034e^{-5(0)}sin(19.36(0)) + 4e^{-5(0)}cos(19.36(0)) + 4 + C = 4 $$

$$0 + 4 + 4 + C = 4 $$

$$C = -4 $$

Plugging our value for C into equation #4 gives us our final expression for i(t) for all times greater than 0 seconds.

Current through inductor (final answer)

$$i_L = i(t) = 1.034e^{-5t}sin(19.36t) + 4e^{-5t}cos(19.36t)$$

$$where: \qquad t \gt 0 $$