For the following circuit...
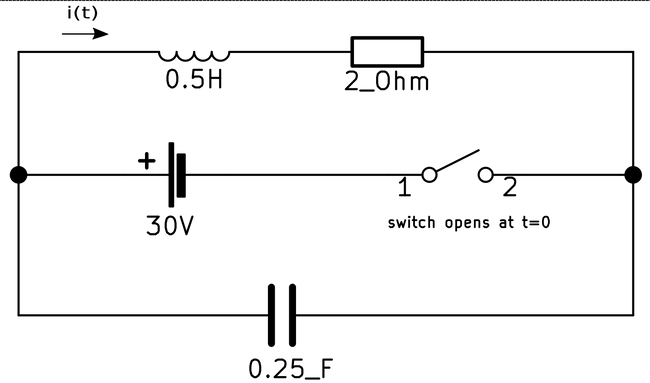
...determine i(t) for t>0.
First, consider the circuit at t>=0:
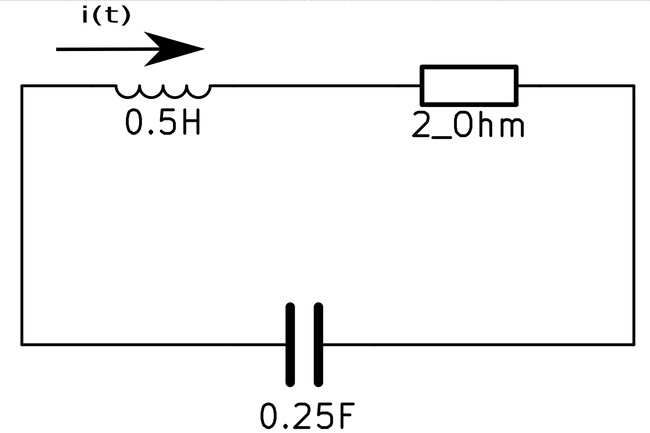
...and recalling the definitions for the voltage of a resistor (R), inductor (L) and capacitor (C):
$$V_R = iR $$
$$V_L = L\frac{di}{dt} $$
$$V_C = \frac{1}{C} \int_{}^{} i \; dt $$
...we proceed to use Kirchoff's Voltage Law by traveling around the loop and obtain the following equation:
$$L\frac{di}{dt} + Ri + \frac{1}{C} \int_{}^{} i \; dt = 0 $$
If we plug our circuit values for L,R and C into the above equation and then take the derivative of it, we get :
$$0.5i'' + 2i' + 4i = 0 $$
Dividing by 0.5 gives us:
$$i'' + 4i' + 8i = 0 \qquad(eqn \; 1)$$
...and just as in the previous page, we recognize eqn #1 as being a 2nd order differential equation. We go about solving it by assuming that solutions are of the following form:
$$i = e^{st} $$
...and where the 1st and 2nd derivatives of i(t) are the following:
$$i' = se^{st} $$
$$i'' = s^2e^{st} $$
If we plug the above 3 expressions into equation #1, we get:
$$s^2e^{st} + 4se^{st} + 8e^{st} = 0 $$
...and dividing through by e^(st):
$$s^2 + 4s + 8 = 0 \qquad ,(Eqn \;2)$$
Eqn #2 is the "characteristic equation of eqn #1. To find the roots of the characteristic equation (values of s) we use the quadratic formula:
$$s = \frac{-b \pm \sqrt[]{b^2-4ac}}{2a} \qquad ,(Quadratic \;formula)$$
$$s = \frac{-4 \pm \sqrt[]{4^2-4(1)(8)}}{2(1)} $$
$$s = \frac{-4 \pm \sqrt[]{-16}}{2} $$
$$s = \frac{-4 \pm j4}{2} $$
$$s = -2 \pm j2$$
...where:
$$s_1=-2+j2 $$
$$s_2=-2-j2 $$
Take note of the fact that since we are dealing with complex roots, we realize that the circuit is under-damped and that solutions to eqn #1 (2nd order diff equ for this circuit) will be of the form:
$$i(t) = Ae^{-\alpha t}cos(t\sqrt{\omega_0^2 - \alpha^2}) + Be^{-\alpha t} sin(t\sqrt{\omega_0^2 - \alpha^2})$$
...where
$$\alpha = \frac{R}{2L} = \; "neper \; frequency"$$
and
$$\omega_0 = \frac{1}{\sqrt{LC}} = \; "resonant \; frequency" \; or \; "undamped \; natural \; frequency"$$
Taking root s1 and plugging it back into our substitution for i(t) gives us:
$$i(t) = e^{s_1t} $$
$$i(t) = e^{t(-2+j2)} $$
$$i(t) = e^{-2t+2tj} $$
$$i(t) = e^{-2t}e^{j2t} $$
Recall Euhler's Identity:
$$e^{j \theta} = cos(\theta) + jsin(\theta) $$
...and if we apply it to the exponential term with the imaginary power, our expression for i(t) becomes:
$$i(t) = e^{-2t}[cos(2t) + jsin(2t)] $$
$$i(t) = e^{-2t}cos(2t) + je^{-2t}sin(2t) $$
We can disregard the imaginary "j" and realize the solutions to our differential equation are represented by the fundamental set:
$$f.s. =[e^{-2t}cos(2t),e^{-2t}sin(2t)] $$
Also remember that any constant multiplied by a solution to a differential equation is also a solution. Our fundamental set becomes:
$$f.s. =[Ae^{-2t}cos(2t),Be^{-2t}sin(2t)] $$
Additionally, recall that given two unique solutions to a 2nd order differential equation, the sum of those two unique solutions is also a solution. This gives us a general solution to eqn #1 of:
$$i(t) = Ae^{-2t}cos(2t) + Be^{-2t}sin(2t) \qquad(general \; solution) $$
Obtain initial conditions i(0), i'(0) and v(0)
The purpose of determining the initial conditions i(0), i'(0) and v(0) is so that we can set up a system of equations that will allow us to solve for the constants (A and B) of our general solution for i(t)
First, let's consider the circuit for t<0 and assume that the switch has been closed for a long enough period of time that we can assume steady state conditions for the circuit. Under steady state conditions, the inductor acts as a short circuit and the capacitor acts as an open circuit. Also note that the voltage across a capacitor and the current through an inductor cannot change instantaneously such that:
$$i_L(0^-) = i_L(0^+) = i_L(0) $$
$$V_C(0^-) = V_C(0^+) = V_C(0) $$
...where "+" and "-" represent points in time immediately before and after the changing of the switch position at t=0.
Such a situation is represented by the circuit below:
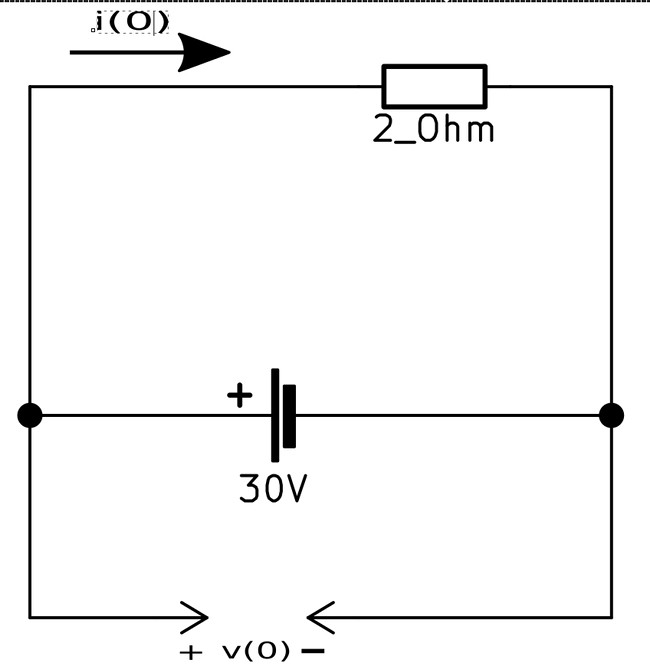
...where i(0) and v(0) represent the current through the inductor and voltage across the capacitor at t=0.
Solving for i(0) and v(0):
$$i(0) = \frac{30}{2} = 15A $$
$$V(0) = 30V $$
Recalling the general solution to our differential equation:
$$i(t) = Ae^{-2t}cos(2t) + Be^{-2t}sin(2t) $$
and our newly discovered value for i(0):
$$i(0) = 15A $$
...by equating the two we get:
$$i(0) = Ae^{-2(0)}cos(2(0)) + Be^{-2(0)}sin(2(0)) = 15 $$
$$i(0) = A + B(0) = 15 $$
$$A = 15 $$
Now take the derivative of our general solution for i(t):
$$i(t) = Ae^{-2t}cos(2t) + Be^{-2t}sin(2t) $$
$$i'(t) = [Ae^{-2t}(-2)sin(2t) + (-2)Ae^{-2t}cos(2t)] $$
$$ \qquad \; \; \; \; + [Be^{-2t}(2)cos(2t) + (-2)Be^{-2t}sin(2t)] $$
$$i'(t) = -2Ae^{-2t}sin(2t) - 2Ae^{-2t}cos(2t) $$
$$ \qquad \; \; \; \; + 2Be^{-2t}cos(2t) - 2Be^{-2t}sin(2t) \qquad ,eqn \;3 $$
We also need to determine a numerical value for i'(0). Using the natural response equivalent circuit for t>=0:

We again use Kirchoff's Voltage Law (KVL) around the circuit. In place of any value of "t", we will use "0" since our eventual goal is a numerical value for i'(0). Also note that the voltage across the capacitor at t=0 has just been determined above {V(0)} and can be substitutes "as is" into our KVL equation. Additionally, don't forget that the "positive" and "negative" terminals of V(0) are oriented the same as the terminals of the 30V source as shown in the circuit where we determined the value of V(0). With all of this in mind, KVL gives us:
$$Li'(0) + Ri(0) - V(0) = 0$$
$$0.5 \; i'(0) + 2(15) - 30 = 0$$
$$0.5 \; i'(0) = 0$$
$$i'(0) = 0$$
Now that we know that i'(0)=0, we can substitute 0 for t in eqn #3 and set it equal to zero. Doing so gives us the following:
$$ -2A + 2B = 0$$
$$ -A + B = 0$$
We already found above that A=15
$$ -15 + B = 0$$
$$ B = 15$$
Having found the values of our constants A and B, we can plug them into our general solution for i(t) thus answering the original question:
$$i(t) = 15e^{-2t}cos(2t) + 15e^{-2t}sin(2t) \qquad for \; t>0 $$
i(t) represents the current through the inductor for all t>0.
In the next example we will look at an RLC series circuit and determine the voltage across the capacitor.
Continue on to RLC series circuit example #2
