Consider the following circuit shown below:
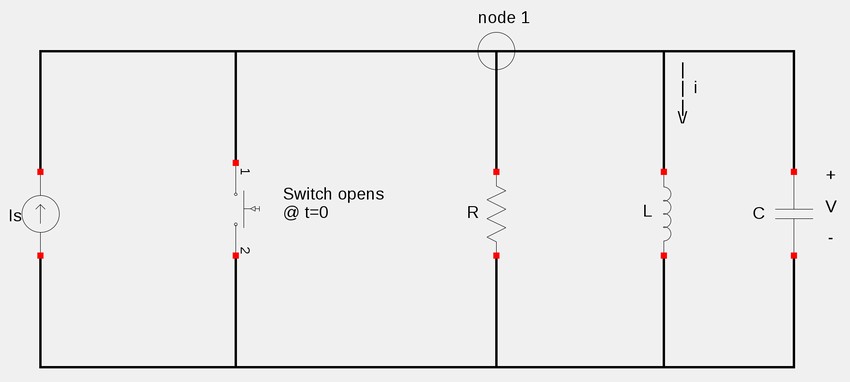
Recall the definition of the current through a capacitor:
$$i_C(t) = Cv'(t) $$
If we apply Kirchoff's Voltage Law (KCL) at node 1, we get the following equation:
$$\frac{v}{R} + i + Cv' = I_s \qquad(Equation \; 1)$$
Notice that:
$$v = v_C = v_L = L\frac{di}{dt} = Li' $$
...and if we substitute the above expression for "v" into equation #1, we get:
$$\frac{L}{R}i' + i + CLi'' = I_s $$
If we rearrange the terms of the above equation and divide through by LC, we get:
$$i'' + \frac{1}{RC}i' + \frac{1}{LC}i = \frac{I_s}{LC} \qquad(Equation \; 2) $$
Equation #2 is a 2nd order non-homogeneous equation which can be solved by either the Annihilator Method or by the Laplace Transform Method. For these step-response circuits, we will use the Laplace Transform Method to solve the differential equation.
Complete solutions to equation #2 consist of a transient response and a steady-state response such that:
$$i(t) = i_t(t) + i_{ss}(t) $$
...where:
$$i_t(t) = transient \; response $$
$$i_{ss}(t) = steady \; state \; response $$
The steady-state response is the final value of i(t) and ends up being the same value of the current source (Is):
$$i_{ss}(t) = I_s$$
Just as with source-free parallel RLC circuits, there are three possible outcomes regarding solutions to equation #2. Note the following substitutions:
$$\alpha = \frac{1}{2RC} $$
$$\omega_0 = \frac{1}{\sqrt{LC}} $$
$$\omega_d = \sqrt{w^2_0 - \alpha^2} $$
Case 1 (Overdamped)
$$\alpha \gt \omega_0 $$
Soultions will be of the form:
$$i(t) = I_s + Ae^{s_1t} + Be^{s_2t} $$
...where s1 and s2 are the roots of the "characteristic equation"
Case 2 (Critically Damped)
$$\alpha = \omega_0 $$
Soultions will be of the form:
$$i(t) = I_s + Ae^{-\alpha t} + Bte^{-\alpha t} $$
Case 3 (Underdamped)
$$\alpha \lt \omega_0 $$
Soultions will be of the form:
$$i(t) = I_s + Ae^{-\alpha t} cos(\omega_d t) + Be^{-\alpha t} sin(\omega_d t) $$
Constants and Initial Conditions
The constants A and B of our solution can be determined via the initial conditions i(0) and i'(0) (if using the Annihilator Method.) Additionally, once we determine the current through the inductor, i(t), we can compute the voltage across the capacitor, v(t), by recognizing that it is the same as the voltage across the inductor (since the two components are in parallel). Thus:
$$v = v_C = v_L = L\frac{di}{dt} = Li'(t) $$
In the next page of this section we will work through an actual example and determine the complete response of a parallel RLC circuit.
Continue on to RLC step response example #1 (parallel RLC)
