For the following circuit, calculate i(t) for all t>0
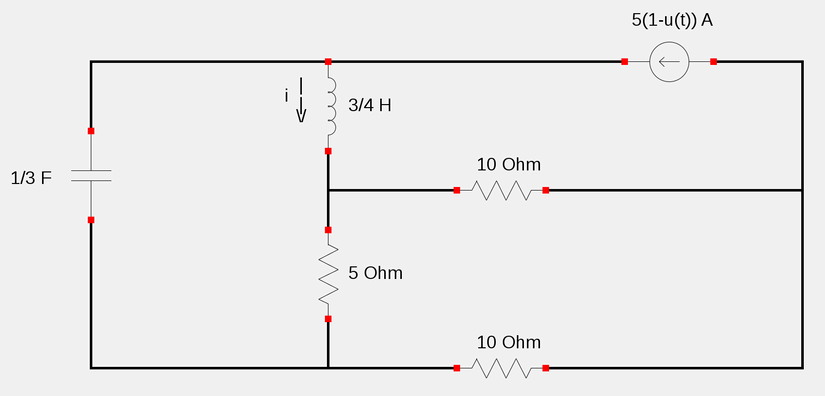
Step 1: Use definition of unit step function to understand behavior of current source
The unit step function (Heaviside Function) is defined as:
$$ u_c(t) = \left\{ \begin{array}{ll} 0 & t \lt c \\ 1 & t \ge c \end{array} \right. \qquad (Definition \; 1) $$
and is somtimes defined via the following form (which is equivalent to the above definition):
$$ u(t-t_0) = \left\{ \begin{array}{ll} 0 & t \lt t_0 \\ 1 & t \ge t_0 \end{array} \right. \qquad (Definition \; 2) $$
...and when plotted looks like this:
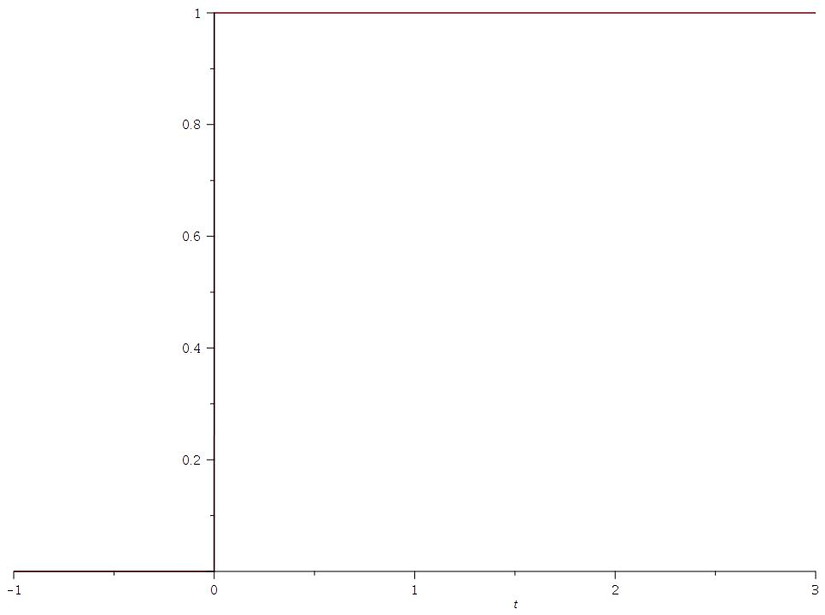
Our current source is given as:
$$5(1-u_0(t)) $$
or:
$$5-5u_0(t) $$
...where c=0 if we are using definition #1
...therefore, the current source is represented by the following expression:
$$5 - 5 \left\{ \begin{array}{ll} 0 & t \lt 0 \\ 1 & t \ge 0 \end{array} \right.$$
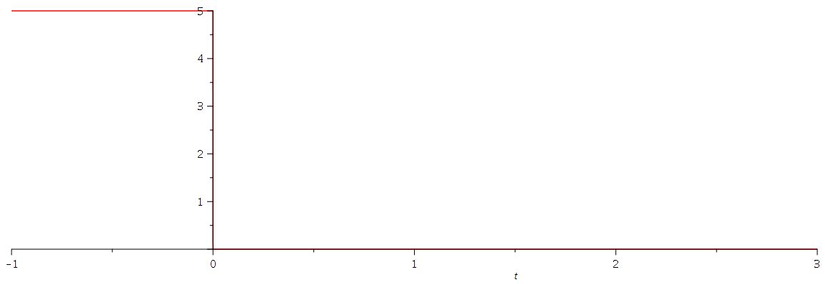
$$= \left\{ \begin{array}{ll} 5 & t \lt 0 \\ 0 & t \ge 0 \end{array} \right. $$
...which can be represented graphically as:
Step 2: Calculate initial conditions i(0), i'(0) and v(0)
Start by considering the circuit for times t<0. At t<0, the current source is 5 Amps. We will assume a time (t) that is sufficiently less than zero so as to be in a steady state condition. Under steady state conditions, the inductor acts as a short circuit and the capacitor an open circuit. Such conditions are shown in the circuit below:
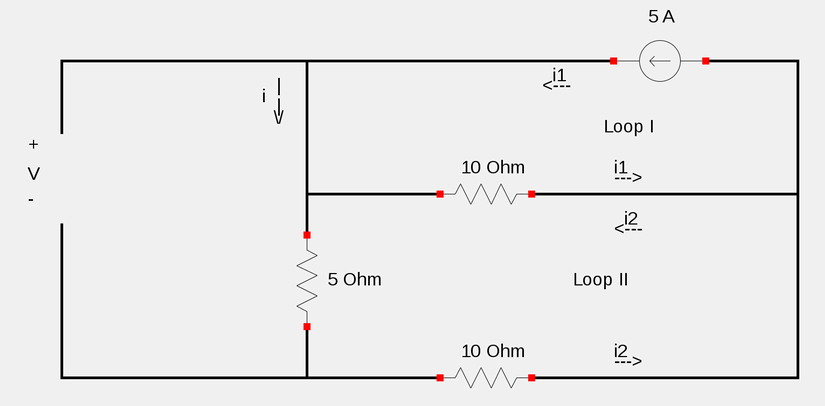
Using the above circuit diagram along with mesh analysis and symbolic mesh currents i1 and i2, we can see that "i1" is 5 Amps. Note that no current flows in the left-most loop due to the capacitor acting as an open circuit. In order to determine i2, we use Kirchoff's Voltage Law (KVL) around loop 2:
$$5i2 + 10i2 + 10(i2-5) = 0 $$
$$i2 = 2A $$
We now see that the voltage across the capacitor (V) is equal to the voltage across the 5 Ohm resistor being that they are in parallel. Additionally, we know that capacitor voltage can't change instantaneously such that:
$$v(0^-) = v(0) = v(0^+) $$
...where "+" and "-" represent times just before and after the change in value of the current source.
Therefor:
$$v(0) = 5(i2) = 5(2) = 10V $$
We also know that the current through an inductor can't change instantaneously such that:
$$i(0^-) = i(0) = i(0^+) $$
...and from the above circuit drawing we see that "i" is equal to the value of the current source (5 Amps).
$$i(0) = 5A $$
In order to determine i'(0) we consider the circuit in it's transient state during times just after t=0, (current source is at 0 Amps):
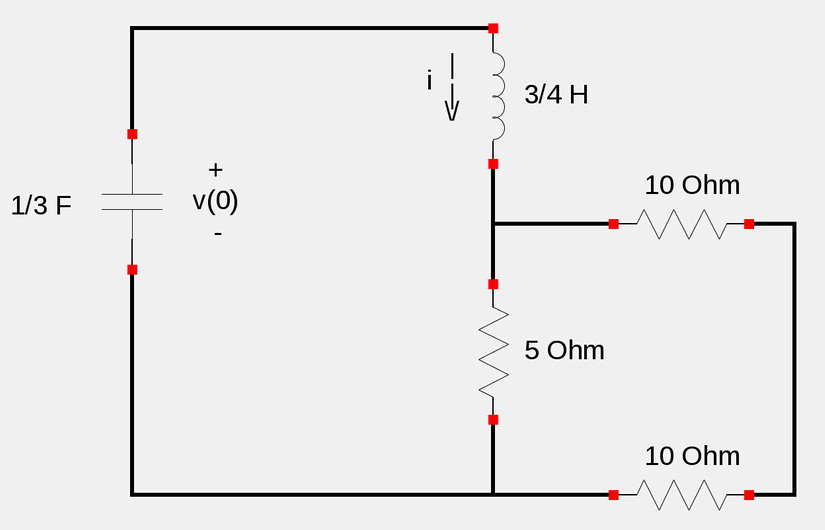
Using the rules of series and parallel resistors allows us to get an equivalent resistance for the three resistors in the lower right of the schematic:
$$R_{eq} = \frac{1}{\frac{1}{5} + \frac{1}{20}} $$
$$R_{eq} = 4 $$
Redrawing the circuit with the above equivalent resistance:
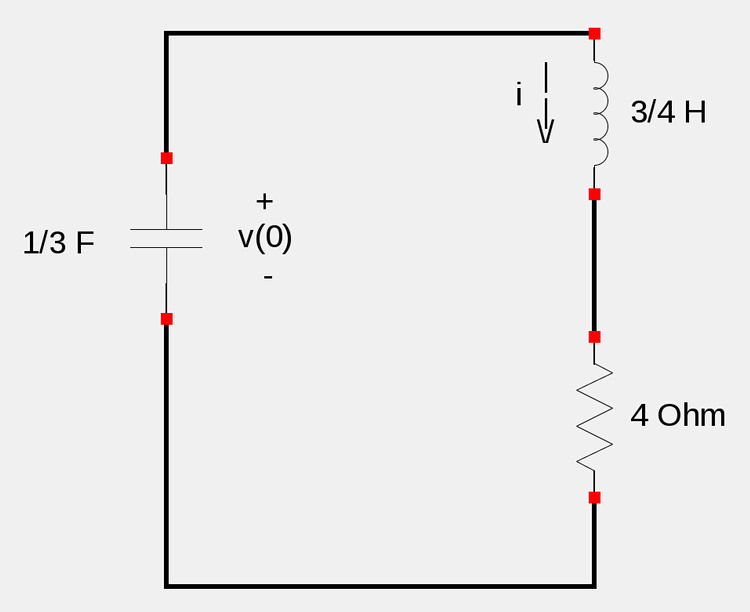
...and recall the following definitions for the voltage across a resistor (R) and inductor (L):
$$V_R = iR $$
$$V_L = L\frac{di}{dt} $$
We now apply KVL to the above circuit and obtain the following equation:
$$Li'(0) + Ri(0) + v(0) = 0 $$
$$\frac{3}{4}i'(0) + 4(5) - 10 = 0 $$
$$i'(0) = -\frac{40}{3} $$
we now have the following initial conditions:
$$i(0) = 5A $$
$$i'(0) = \frac{-40}{3} $$
$$v(0) = 10v $$
Step 3: Obtain a differential equation representing the circuit in it's transient state at times t>0:
Using the following schematic:

...as well as the following definitions for the voltage across a resistor (R), inductor (L) and capacitor (C):
$$V_R = iR $$
$$V_L = L\frac{di}{dt} $$
$$V_C = \frac{1}{C} \int_{}^{} i \; dt $$
...we use KVL around the loop and obtain the following equation:
$$Li' + Ri + v(0) + \frac{1}{C} \int_{}^{} i \; dt = 0 $$
$$\frac{3}{4}i' + 4i + 10 + 3 \int_{}^{} i \; dt = 0 $$
Taking the derivative of the above equation gives us:
$$\frac{3}{4}i'' + 4i' + 3i = 0 $$
Multiply through by 4/3:
$$i'' + \frac{16}{3}i' + 4i = 0 \qquad(Eqn \; 1)$$
Equation #1 is a second order differential equation in terms of i(t).
Step 4: Solve Equation #1 using the Laplace Transform method
This step makes use of the information used the Differential Equations with Laplace Transform section as well as the table of elementary Laplace Transforms provided here . We start by taking the Laplace Transform of both sides of equation #1.
$$\mathcal{L}(i'') + \frac{16}{3}\mathcal{L}(i') + 4\mathcal{L}(i) = \mathcal{L}(0)$$
Using the table as a reference, we expand the above expression:
$$s^2\mathcal{L}(i) - si(0) - i'(0) + \frac{16}{3}[s\mathcal{L}(i) - i(0)] + 4\mathcal{L}(i) = 0 $$
Recall two of our initial conditions:
$$i(0) = 5A $$
$$i'(0) = \frac{-40}{3} $$
...and substitute them into the above expression and then expand it to get:
$$s^2\mathcal{L}(i) - 5s + \frac{40}{3} + \frac{16}{3}s\mathcal{L}(i) - \frac{80}{3} + 4\mathcal{L}(i) = 0 $$
...which condenses to:
$$\mathcal{L}(i)[s^2 + \frac{16}{3}s + 4] - 5s - \frac{40}{3} = 0 $$
Now isolate the Laplace term on one side of the equation:
$$\mathcal{L}(i) = (5s + \frac{40}{3})(\frac{1}{s^2 + \frac{16}{3}s + 4}) $$
...and multiply the two terms in parenthesis:
$$\mathcal{L}(i) = 5\Big[\frac{s}{s^2+\frac{16}{3}s+4}\Big] + \frac{40}{3}\Big[\frac{1}{s^2+\frac{16}{3}s+4}\Big] \qquad(Equation \; 2)$$
Next, we have to use some intuition and realize that eventually we will be taking the inverse Laplace Transform of the right side of the equation (in order to solve for "i"). In order to do so, we need to make the right side look like something that resembles the 2nd and 4th columns of the Laplace Transform table. Factoring the denominator of both terms would be a good start, but they are not factor-able. Therefor we will proceed by "completing the square."
Side-work (completing the square):
$$s^2 + \frac{16}{3}s + 4 $$ $$\qquad = \Big[s^2 + \frac{16}{3}s + \bigg(\frac{\frac{16}{3}}{2}\bigg)^2\Big] + 4 - \bigg(\frac{\frac{16}{3}}{2}\bigg)^2 $$ $$\qquad = (s^2 + \frac{16}{3}s + \frac{64}{9}) - \frac{28}{9}$$ $$\qquad = (s + \frac{8}{3})^2 - \frac{28}{9}$$
After completing the square, we substitute our result into the denominator of equation #2:
$$\mathcal{L}(i) = 5\Big[\frac{s}{(s + \frac{8}{3})^2 - \frac{28}{9}}\Big] + \frac{40}{3}\Big[\frac{1}{(s + \frac{8}{3})^2 - \frac{28}{9}}\Big] $$
...and take the inverse Laplace Transform of both sides of the equation:
$$i = 5\mathcal{L^{-1}}\Big[\frac{s}{(s + \frac{8}{3})^2 - \frac{28}{9}}\Big] + \frac{40}{3}\mathcal{L^{-1}}\Big[\frac{1}{(s + \frac{8}{3})^2 - \frac{28}{9}}\Big]$$
Once again we need a degree of intuition to see that both inverse Laplace Transform terms somewhat resemble relations #21 and #22 on our table. The more of these types of problems you do, the easier it is to see a "roadmap" ahead for solving them, and there is no magical technique aside from "practice makes perfect." The "s" term in the numerator of the inverse term left of the "+" sign leads us to try and make it look like the right column of item #21 in the table. Start by realizing that we can rewrite the numerator as:
$$s = (s+\frac{8}{3}) - \frac{8}{3} $$
...which gives us:
$$i = 5\mathcal{L^{-1}}\Big[\frac{(s+\frac{8}{3}) - \frac{8}{3}}{(s + \frac{8}{3})^2 - \frac{28}{9}}\Big] + \frac{40}{3}\mathcal{L^{-1}}\Big[\frac{1}{(s + \frac{8}{3})^2 - \frac{28}{9}}\Big] $$
You may also see that the 2nd inverse Laplace term somewhat resembles item #22 in the table. If we multiply 40/3 by 3/sqrt(28), it will have the form of #22 and still be equivalent to the above expression. Therefor, we now have:
$$i = 5\mathcal{L^{-1}}\Big[\frac{(s+\frac{8}{3}) - \frac{8}{3}}{(s + \frac{8}{3})^2 - \frac{28}{9}}\Big] + \frac{40}{3}\Big(\frac{3}{\sqrt{28}} \Big)\mathcal{L^{-1}}\Big[\frac{\frac{\sqrt{28}}{3}}{(s + \frac{8}{3})^2 - \frac{28}{9}}\Big] $$
If we expand out the above, we get:
$$i = 5\mathcal{L^{-1}}\Big[ \frac{s+\frac{8}{3}}{(s+\frac{8}{3})^2-\frac{28}{9}} \Big] - 5\mathcal{L^{-1}}\Big[ \frac{\frac{8}{3}}{(s+\frac{8}{3})^2-\frac{28}{9}} \Big] $$
$$\qquad \qquad + \frac{40}{\sqrt{28}}\mathcal{L^{-1}}\Big[\frac{\frac{\sqrt{28}}{3}}{(s + \frac{8}{3})^2 - \frac{28}{9}}\Big] $$
In order to make the 2nd inverse Laplace term resemble item 21 in the table, we multiply it by 8/sqrt(28):
$$i = 5\mathcal{L^{-1}}\Big[ \frac{s+\frac{8}{3}}{(s+\frac{8}{3})^2-\frac{28}{9}} \Big] - 5 \Big(\frac{8}{\sqrt{28}} \Big) \mathcal{L^{-1}}\Big[ \frac{\frac{\sqrt{28}}{3}}{(s+\frac{8}{3})^2-\frac{28}{9}} \Big] $$
$$\qquad \qquad + \frac{40}{\sqrt{28}}\mathcal{L^{-1}}\Big[\frac{\frac{\sqrt{28}}{3}}{(s + \frac{8}{3})^2 - \frac{28}{9}}\Big] $$
...which gives us:
$$i = 5\mathcal{L^{-1}}\Big[ \frac{s+\frac{8}{3}}{(s+\frac{8}{3})^2-\frac{28}{9}} \Big] - \frac{40}{\sqrt{28}} \mathcal{L^{-1}}\Big[ \frac{\frac{\sqrt{28}}{3}}{(s+\frac{8}{3})^2-\frac{28}{9}} \Big] $$
$$\qquad \qquad + \frac{40}{\sqrt{28}}\mathcal{L^{-1}}\Big[\frac{\frac{\sqrt{28}}{3}}{(s + \frac{8}{3})^2 - \frac{28}{9}}\Big] \qquad(Equation \; 3)$$
We can now see that the first term of our expression for i resembles item #22 in the table while the 2nd and 3rd terms resemble item #21. If we use our table to solve for the inverse Laplace transform terms, we see that:
$$A) \; \; \mathcal{L^{-1}}\Big[ \frac{s+\frac{8}{3}}{(s+\frac{8}{3})^2-\frac{28}{9}} \Big] = e^{-\frac{8}{3}t}cosh \Big(\frac{\sqrt{28}}{3}t \Big)$$ ...where by item #22: $$\qquad a=-\frac{8}{3} \qquad, \; b=\frac{\sqrt{28}}{3}$$
$$B) \; \; \mathcal{L^{-1}}\Big[ \frac{\frac{\sqrt{28}}{3}}{(s+\frac{8}{3})^2-\frac{28}{9}} \Big] = e^{-\frac{8}{3}t}sinh\Big( \frac{\sqrt{28}}{3}t \Big)$$ ...where by item #21: $$\qquad a=-\frac{8}{3} \qquad, \; b=\frac{\sqrt{28}}{3}$$
If we plug our two above expressions (A, B) into equation #3, we get:
$$i = 5A - \frac{40}{\sqrt{28}}B + \frac{40}{\sqrt{28}}B = i(t)$$
$$ i(t) = 5A $$
$$i(t) = 5e^{-\frac{8}{3}t} cosh\Big( \frac{\sqrt{28}}{3}t \Big) \qquad(Equation \; 4)$$
Recall the definition of hyperbolic cosine: $$cosh(x) = \frac{e^x+e^{-x}}{2} $$ ...and apply it to equation #4 (utilizing the rules of exponents):
$$i(t) = 5e^{-\frac{8}{3}t} \Big[\frac{e^{\frac{\sqrt{28}}{3}t} + e^{-\frac{\sqrt{28}}{3}t}}{2} \Big] $$
$$i(t) = \frac{5}{2} \Big[e^{\frac{\sqrt{28}}{3}t - \frac{8}{3}t} + e^{-\frac{\sqrt{28}}{3}t - \frac{8}{3}t} \Big] $$
At long last, we have our final expression for i(t) for all t>0:
$$i(t) = 2.5e^{-0.903t} + 2.5e^{-4.43t} $$
