For the following circuit...

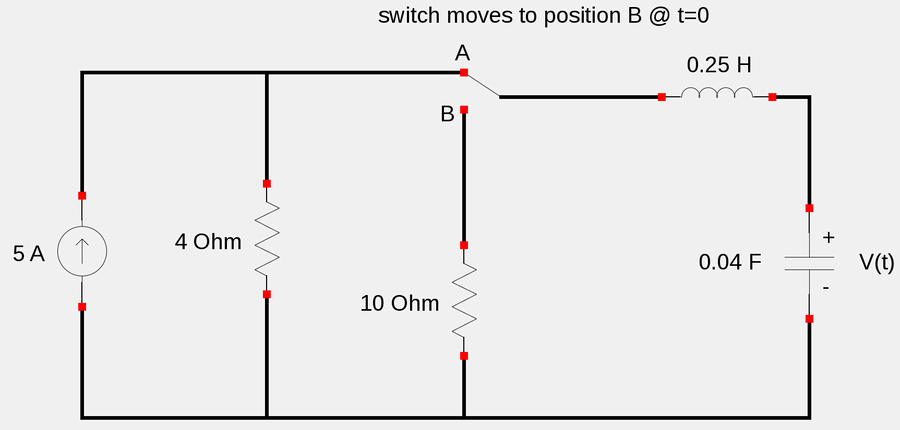
Find v(t) for all t>=0

First lets obtain a second order differential equation that represents the natural response of the RLC circuit. The natural response occurs at t>=0 and the current source is effectively disconnected. (as shown below):

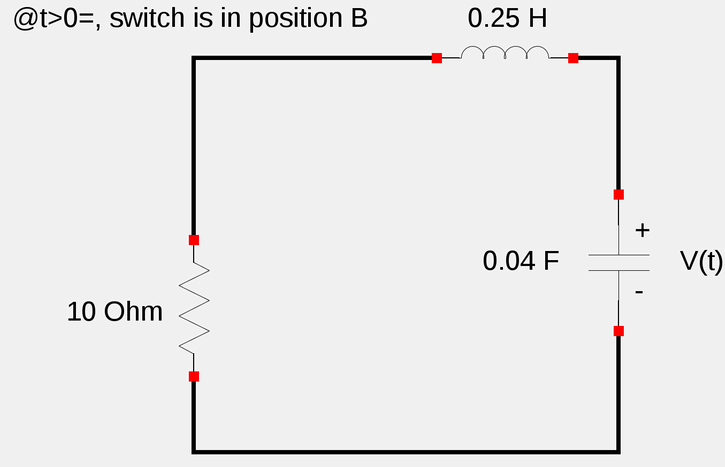
By using Kirchoff's Voltage law and as well as the following definitions of voltage for our 3 circuit components:

$$V_R = iR $$

$$V_L = L\frac{di}{dt} $$

$$V_C = \frac{1}{C} \int_{}^{} i \; dt $$

...we obtain the following 2nd order differential equation by summing the individual voltages as we travel around the circuit:

$$10i + 0.25i' + \frac{1}{0.04}\int {}^{}i \; dt = 0 $$

By taking the derivative of the above equation, rearranging terms and dividing through by 0.25, we get:

$$i'' + 40i' + 100i = 0 \qquad , \; (Eqn \;1) $$

Equation 1 is a 2nd order differential equation. Once again we go about solving it by assuming that solutions are of the following form:

$$i = e^{st} $$

...and where the 1st and 2nd derivatives of i(t) are the following:

$$i' = se^{st} $$

$$i'' = s^2e^{st} $$

Substituting the above three expressions into eqn 1 gives us:

$$s^2e^{st} + 40se^{st} + 100e^{st} = 0 $$

We can divide out the exponential terms

$$s^2 + 40s + 100 = 0 \qquad , \; (Eqn \;2) $$

Eqn #2 is the "characteristic equation of eqn #1. To find the roots of the characteristic equation (values of s) we use the quadratic formula:

$$s = \frac{-b \pm \sqrt[]{b^2-4ac}}{2a} \qquad ,(Quadratic \;formula)$$

$$s = \frac{-40 \pm \sqrt[]{-40^2-4(1)(100)}}{2(1)}$$

$$s = -20 \pm 17.32 $$

$$s_1 = -2.680$$

$$s_2 = -37.32 $$

Substituting s1 and s2 into our definition for i(t) gives us the 2 solution fundamental set of:

$$f.s. = \{e^{-2.680t}, e^{-37.32t}\} $$

Recall that for a 2nd order Homogeneous differential equation, any constant multiplied by a solution is also a solution. Therefore:

$$f.s. = \{Ae^{-2.680t}, Be^{-37.32t}\} $$

Additionally, given two unique solutions to a 2nd order homogeneous differential equation, the sum of those two unique solutions is also a solution. Therefor, the general solution to equation #1 is the following:

$$i(t) = Ae^{-2.680t} + Be^{-37.32t} \qquad (Eqn \; 3)$$

Solving for constants A and B

In order to solve for the constants of equation #3 (our general solution), we will need to determine numerical values for i(0) and i'(0). In order to do so let's consider the circuit at t<0 (as shown below):

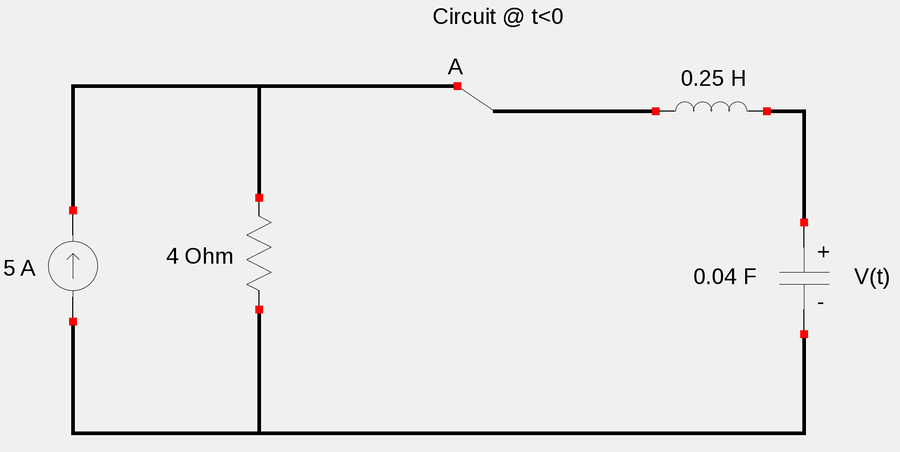
In order to simplify things (and refresh some basic skills), let's use a source transformation technique to convert the above current source, which is in parallel with the 4 Ohm resistor, into a voltage source in series with the 4 Ohm resistor. While Thevenin and Norton equivalent circuits aren't explained in detail here, we will proceed as follows:

$$R_{TH} = 4 $$

$$I_N = 5 $$

$$V_{TH} = R_{TH}(I_N) = 5(4) = 20V$$

This gives us the following equivalent circuit:

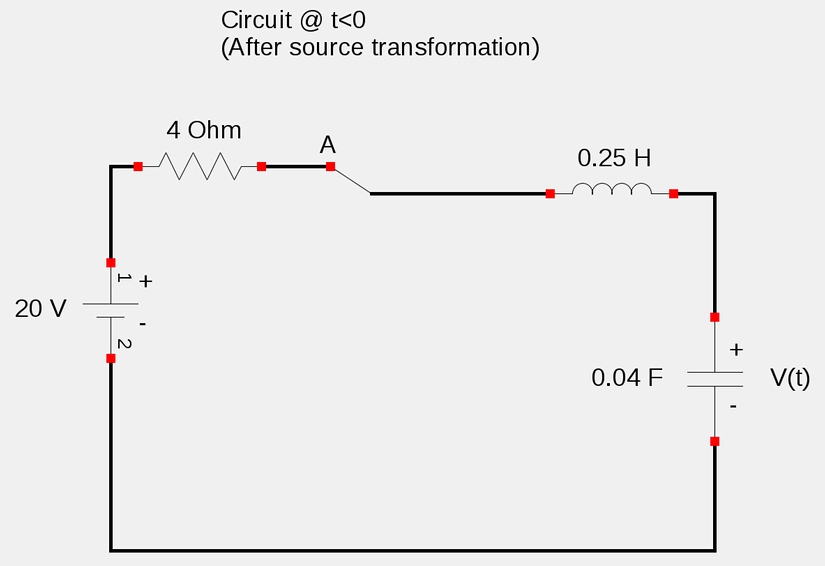
We will assume that the switch has been in position A for a long enough time to display steady-state characteristics. We know that in such conditions the inductor acts as a short while the capacitor acts as an open circuit. Such condtions for the circuit are represented below:

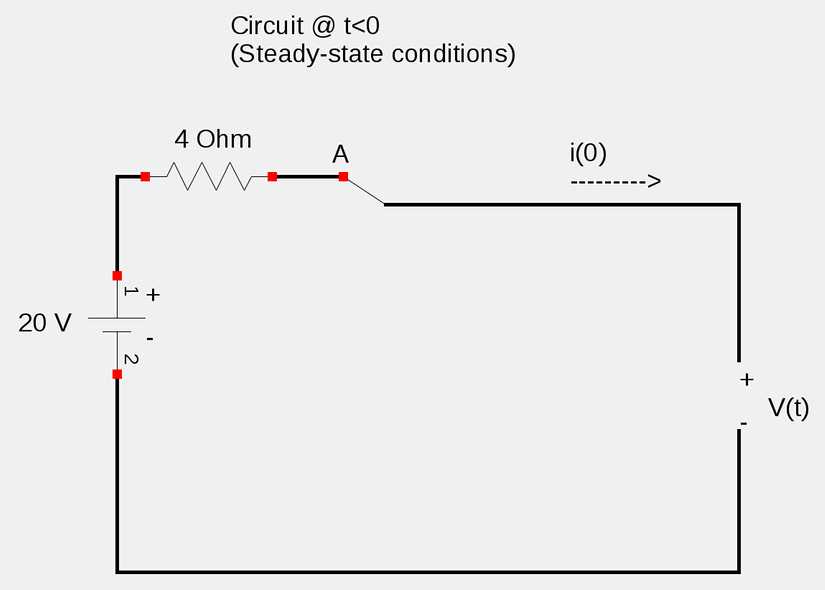
We also recall that inductor current and capacitor voltage can't change instantaneously such that:

$$i(0^-) = i(0) = i(0^+) $$

$$v(0^-) = v(0) = v(0^+) $$

...where the positive and negative signs represent times just before and just after the changing of the switch position. Therefor:

$$i(0) = 0A $$

$$v(0) = 20 V $$

In order to find a numerical value for i'(0), we will revisit our circuit at t>=0 (as shown below):

...and using Kirchoff's Voltage law around the circuit for time t=0 gives us:

$$Ri(0) + Li'(0) + v(0) = 0 $$

$$10(0) + 0.25i'(0) + 20 = 0 $$

$$0.25i'(0) = -20 $$

$$i'(0) = -80 $$

Knowing values for i(0) and i'(0), we can proceed to set up a system of 2 equations and two unknowns:

$$i(0) = Ae^{-2.68(0)} + Be^{-37.32(0)} = 0 $$

$$A + B = 0 \qquad(Eqn \; 4) $$

Taking the derivative of eqn 3:

$$i(t) = Ae^{-2.680t} + Be^{-37.32t} $$

$$i'(t) = -2.68Ae^{-2.680t} -37.32 Be^{-37.32t} $$

...and setting it equal to zero:

$$i'(0) = -2.68Ae^{-2.680(0)} -37.32 Be^{-37.32(0)} = -80$$

$$-2.68A -37.32 B = -80 \qquad(Eqn \; 5)$$

Using whatever technique you prefer to solve the system of equations for equations 4 and 5 gives you the following values for A and B

$$A = -2.31 $$

$$B = 2.31 $$

...which gives us the final expression for i(t) for all t>0 :

$$i(t) = 2.31e^{-37.32t} - 2.31e^{-2.68t} $$

Finding v(t):

Recall the definition for voltage across a capacitor:

$$v(t) = V_0 + \frac{1}{c} \int_{}^{} i \; dt $$

...and substituting our above determined numerical value for v(0) as well as c (capacitor value) and expression for i(t):

$$v(t) = 20 + \frac{1}{0.04} \int{}^{} [2.31e^{-37.32t} - 2.31e^{-2.68t}]dt $$

$$ v(t) = 20 + 25[-0.0619e^{-37.32t} + 0.8619e^{-2.68t} + C] $$

$$ v(t) = 20 + 25C - 1.548e^{-37.32t} + 21.55e^{-2.68t} \qquad(Eqn \; 6)$$

Now we will determine the constant of integration (C) by again using our above determined numerical value for v(0)

$$ v(0) = 20 + 25C - 1.548e^{-37.32(0)} + 21.55e^{-2.68(0)} = 20$$

$$ 20 + 25C - 1.548 + 21.55 = 20 $$

$$25C + 40 = 20 $$

$$C = -0.8 $$

We now substitute the above value for C into equation #6:

$$v(t) = 20 + 25(-0.8) - 1.548e^{-37.32t} + 21.55e^{-2.68t} $$

...And we get our final expression for v(t) for all t>0 (rounded to three significant figures):

$$v(t) = 21.6e^{-2.68t} - 1.55e^{-37.3t}$$