For the following circuit:
All values are RMS
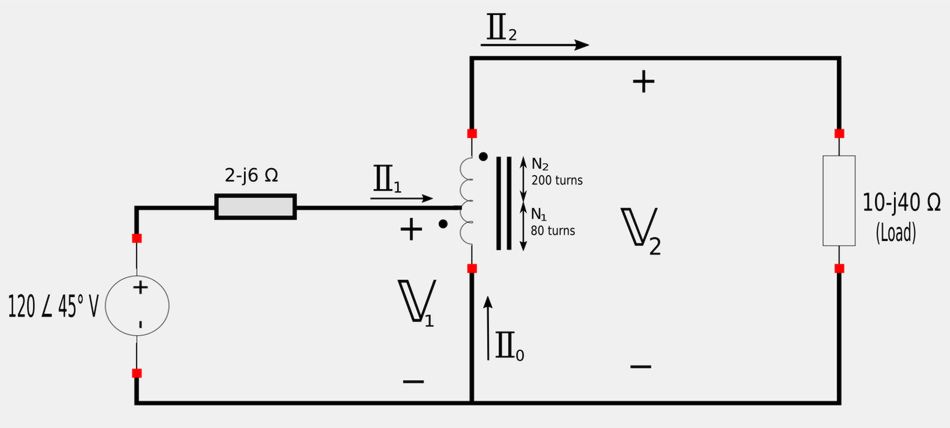
- A) Calculate I1, I2 and I0.
- B) Determine the average power delivered to the load.
A) Calculate current values
Recall the turns ratio expression for the primary and secondary voltages of a step-up autotransformer: $$ \frac{\mathbb{V}_2}{\mathbb{V}_1} = \frac{N_1+N_2}{N_1} $$ For our example we will get the following: $$ \frac{\mathbb{V}_2}{\mathbb{V}_1} = \frac{280}{80} = 3.5 $$ If we express V1 in terms of V2 we get: $$ \mathbb{V}_1 = \frac{\mathbb{V}_2}{3.5} \qquad ,(Eqn\;1) $$ Now, recall the turns ratio expression for the primary and secondary currents of a step-up autotransformer: $$ \frac{\mathbb{I}_2}{\mathbb{I}_1} = \frac{N_1}{N_1+N_2} $$ For our example we have: $$ \frac{\mathbb{I}_2}{\mathbb{I}_1} = \frac{80}{280} = \frac{1}{3.5} $$ If we express I1 in terms of I2 we get: $$ \mathbb{I}_1 = 3.5\mathbb{I}_2 \qquad ,(Eqn\;2)$$
Apply Kirchhoff's Voltage Law (KVL) to the primary side:
$$ \mathbb{I}_1(2-j6) + \mathbb{V}_1 = 120\angle 45^{\circ} $$ $$ 6.325\;\mathbb{I}_1 \angle 288.4^{\circ} + \mathbb{V}_1 = 120\angle 45^{\circ} $$ Substitute equations 1 and 2 into the above expression and get the following: $$ (6.325 \angle 288.4^{\circ})(3.5\;\mathbb{I}_2)+\frac{\mathbb{V}_2}{3.5} = 120\angle 45^{\circ} $$ $$ 22.14\;\mathbb{I}_2 \angle 288.4^{\circ} + 0.2857\; \mathbb{V}_2 = 120\angle 45^{\circ} \qquad ,(Eqn\;A) $$
Apply (KVL) to the secondary side:
$$ \mathbb{I}_2(10+j40) - \mathbb{V}_2 = 0 $$ $$ 41.23\;\mathbb{I}_2 \angle 75.96^{\circ} - \mathbb{V}_2 = 0 \qquad ,(Eqn\;B)$$
Solve equations A and B:
We will use Cramer's Rule to solve for I2 and V2 in equations A and B. First put the equations in matrix form: $$ \begin{pmatrix} 22.14\angle 288.4^{\circ}&0.2857&120\angle 45^{\circ}\\ 41.23 \angle 75.96^{\circ}&-1&0\\ \end{pmatrix} $$ Now calculate the required determinants: $$ D = \begin{vmatrix} 22.14\angle 288.4^{\circ}&0.2857\\ 41.23 \angle 75.96^{\circ}&-1\\ \end{vmatrix} = 13.74 \angle 135.8^{\circ} $$ $$ D_{\mathbb{I}_2} = \begin{vmatrix} 120\angle 45^{\circ}&0.2857\\ 0&-1\\ \end{vmatrix} = 120 \angle 225^{\circ} $$ $$ D_{\mathbb{V}_2} = \begin{vmatrix} 22.14\angle 288.4^{\circ}&120\angle 45^{\circ}\\ 41.23 \angle 75.96^{\circ}&0\\ \end{vmatrix} = 4948 \angle 301^{\circ} $$ Now calculate V2 and I2: $$ \mathbb{V}_2 = \frac{D_{\mathbb{V}_2}}{D} = \frac{4948 \angle 301^{\circ}}{13.74 \angle 135.8^{\circ}} $$ $$ \mathbb{V}_2 = 360.1 \angle 165.2 \; V $$ $$ \mathbb{I}_2 = \frac{D_{\mathbb{I}_2}}{D} = \frac{120 \angle 225^{\circ}}{13.74 \angle 135.8^{\circ}} $$
$$ \mathbb{I}_2 = 8.734 \angle 89.2^{\circ} \; A $$
Calculate remaining current values:
Using equation #2 and the value we just determined for I2, calculate I1: $$ \mathbb{I}_1 = 3.5\mathbb{I}_2 = 3.5(8.734 \angle 89.2^{\circ}) $$
$$ \mathbb{I}_1 = 30.57 \angle 89.22^{\circ} \; A $$
Now apply Kirchhoff's Current Law (KCL) at the transformer tap: $$ \mathbb{I}_1 + \mathbb{I}_0 = \mathbb{I}_2 $$ $$ \mathbb{I}_0 = \mathbb{I}_2 - \mathbb{I}_1 $$ $$ \;\;\; = (8.734 \angle 89.2^{\circ}) - (30.57 \angle 89.22^{\circ}) $$
$$ \mathbb{I}_0 = 21.84\angle 269.2^{\circ} \; A $$
Determine the average power delivered to load
Recall from our derived expressions for complex power, that when dealing with RMS values, we can use the following: $$ \mathbb{S} = \mathbb{V}_{rms} \mathbb{I}_{rms}* $$ So, for the complex power delivered to the load in our circuit (and remembering that all calculated values have been RMS) we would have: $$ \mathbb{S}_L = \mathbb{V}_2 \mathbb{I}_2* $$ $$ \;\;\;\; = [360.1 \angle 165.2][8.734 \angle (-89.2^{\circ})] $$ $$ \mathbb{S}_L = 3145\angle 76^{\circ} = 760.9+j3052 $$ Finally, we know that the average power (or real power) equates to: $$ P_L = R_e \{ \mathbb{S}_L \} = R_e \{ 760.9+j3052 \} $$
$$ P_L = 760.9 \; W $$
Next we will look at an example problem involving a step-down autotransformer.
Continue on to autotransformers (step-down example problem)...
