For the following circuit, calculate the average power delivered to the load.
All values are RMS
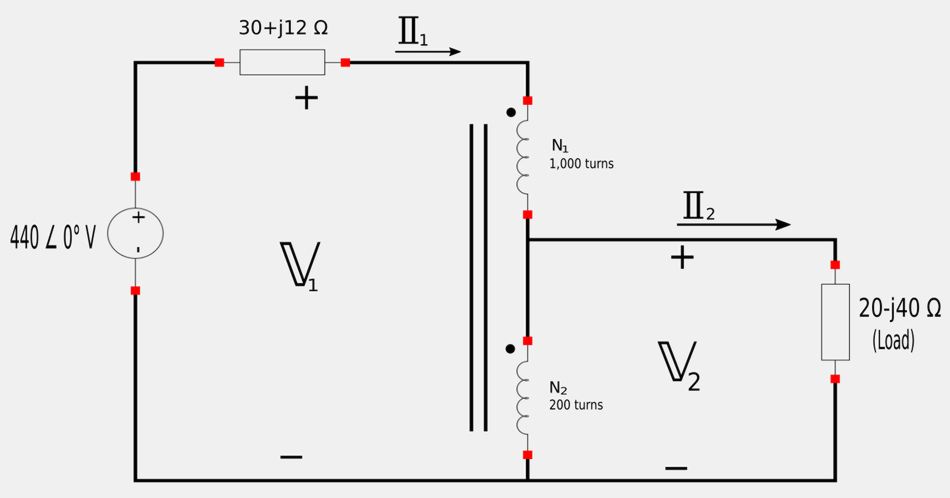
Recall the turns ratio expression for the primary and secondary voltages of a step-down autotransformer: $$ \frac{\mathbb{V}_2}{\mathbb{V}_1} = \frac{N_2}{N_1+N_2} $$ For our circuit this gives us: $$ \frac{\mathbb{V}_2}{\mathbb{V}_1} = \frac{200}{1200} = \frac{1}{6} $$ V1 in terms of V2 gives us: $$ \mathbb{V}_1 = 6\mathbb{V}_2 \qquad,(Eqn\;1) $$ Now, recall the turns ratio expression for the primary and secondary currents of a step-down autotransformer: $$ \frac{\mathbb{I}_2}{\mathbb{I}_1} = \frac{N_1+N_2}{N_2} $$ For our circuit this gives us: $$ \frac{\mathbb{I}_2}{\mathbb{I}_1} = \frac{1200}{200} = 6 $$ I1 in terms of I2 gives us: $$ \mathbb{I}_1 = \frac{\mathbb{I}_2}{6} \qquad,(Eqn\;2) $$
Apply Kirchhoff's Voltage Law (KVL) to primary and secondary side.
For the primary we have: $$ \mathbb{I}_1(30+j12)+\mathbb{V}_1 = 440 $$ $$ 32.31\;\mathbb{I}_1 \angle 21.8^{\circ}+\mathbb{V}_1 = 440 $$ Substitute equations 1 and 2 into the above expression: $$ (32.31 \angle 21.8^{\circ}) \Big( \frac{\mathbb{I}_2}{6} \Big)+6\mathbb{V}_2 = 440 $$ $$ 5.385\;\mathbb{I}_2 \angle 21.8^{\circ} + 6\mathbb{V}_2 = 440 \qquad,(Eqn\;A) $$ Applying KVL to the secondary side gives us: $$ \mathbb{I}_2(20-j40) - \mathbb{V}_2 = 0 $$ $$ 44.72 \; \mathbb{I}_2 \angle 296.6^{\circ} - \mathbb{V}_2 = 0 \qquad,(Eqn\;B) $$
Solve equations A and B.
I won't walk through the steps of solving the equations since the method is the same as in the step-up example problem. Using whatever technique you choose (substitution, Cramer's Rule, matrix row operations, etc...) will give you the following value for current I2: $$ \mathbb{I}_2 = 1.638\angle 62.3^{\circ} \; A $$
Calculate the power delivered to the load.
Converting the load impedance from rectangular to polar form gives us: $$ \mathbb{Z}_L = 20-j40 = 44.72\angle 296.6^{\circ} \; \Omega $$ Recognizing that our voltage and current values are RMS, and recalling the expressions for complex power, we realize that we can express the complex power delivered to the load as: $$ \mathbb{S} = I_{rms}^2 \mathbb{Z} $$ For our circuit we have: $$ \mathbb{S}_L = (I_2)^2 \mathbb{Z}_L = (1.638)^2(44.72\angle 296.6^{\circ}) $$ $$ \mathbb{S}_L = 120\angle 296.6^{\circ} = 53.72-j107.3 $$ The real/average power delivered to the load is defined as: $$ P_L = R_e \{ \mathbb{S}_L \} = R_e \{ 53.72-j107.3 \} $$
$$ P_L = 53.7 \; W $$
