For circuits involving ideal transformers, the transformer can be eliminated by reflecting sources and impedances from the secondary side to the primary (and vice-versa).
Reflecting secondary to primary
Consider the following circuit:

Determine Thevenin equivalent to the right of terminals a-b
Our plan of attack for reflecting the secondary side to the primary will be to determine the Thevenin equivalent circuit to the right of the a-b terminals. The Thevenin voltage will be the open-circuit voltage at the a-b terminals:
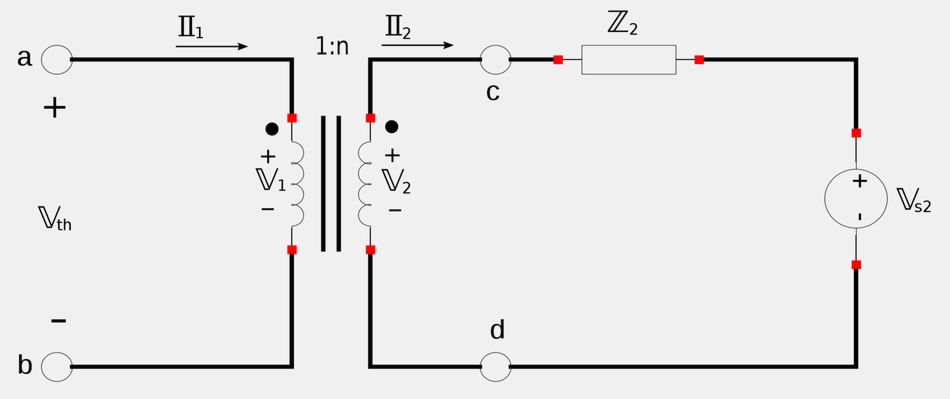
We see that : $$ \mathbb{V}_{th} = \mathbb{V}_1 $$ Also, since we have an open circuit on the primary side then: $$ \mathbb{I}_1 = 0 $$ Recalling the expressions for the turns ratio, we know that: $$ \mathbb{I}_2 = \frac{\mathbb{I}_1}{n} $$ ...which means that: $$ \mathbb{I}_2 = 0 $$ ...and if I2 = 0, then: $$ \mathbb{V}_2 = \mathbb{V}_{s2} $$ Again, recalling the expressions for the turns ratio, we know that: $$ \mathbb{V}_1 = \frac{\mathbb{V}_2}{n} $$ We can now express the Thevenin voltage as:
$$ \mathbb{V}_{th} = \mathbb{V}_1 = \frac{\mathbb{V}_2}{n} = \frac{\mathbb{V}_{s2}}{n} $$
In order to determine the Thevenin impedance, we remove the voltage source in the secondary and insert a dummy 1V source at terminals a-b.
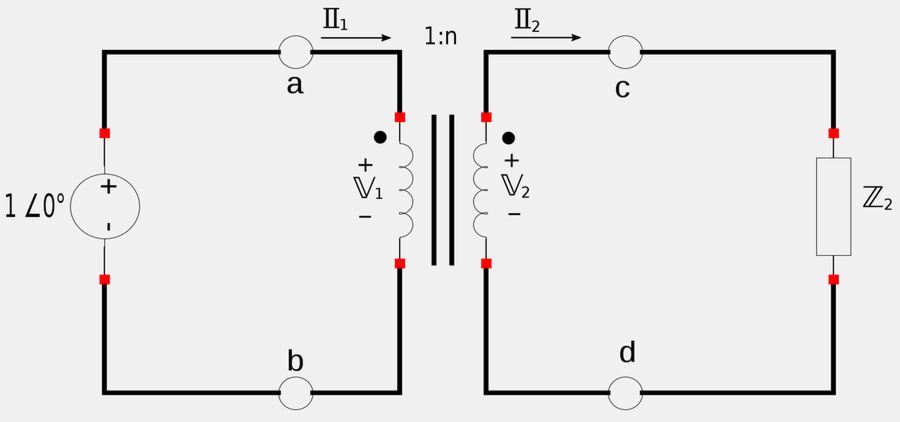
The Thevenin impedance will be defined as: $$ \mathbb{Z}_{th} = \frac{\mathbb{V}_1}{\mathbb{I}_1} $$ However, we know that: $$ \mathbb{I}_1 = n\mathbb{I}_2 \quad, \mathbb{V}_1 = \frac{\mathbb{V}_2}{n} $$ Therefore: $$ \mathbb{Z}_{th} = \frac{\mathbb{V}_2}{n} \Big( \frac{1}{n\mathbb{I}_2} \Big) = \frac{\mathbb{V}_2}{n^2 \mathbb{I}_2} $$ But: $$ \qquad \frac{\mathbb{V}_2}{\mathbb{I}_2} = \mathbb{Z}_2 $$ So finally we have a Thevenin impedance of:
$$ \mathbb{Z}_{th} = \frac{\mathbb{Z}_2}{n^2} $$
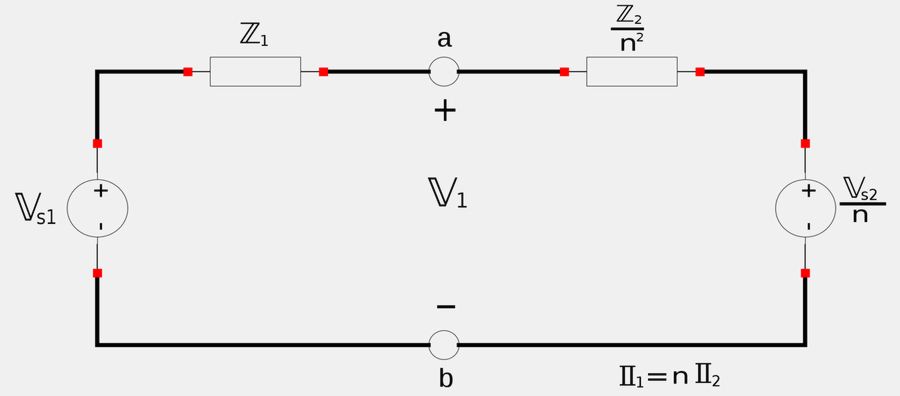
We now add the Thevenin equivalent circuit to the right side of terminals a-b in the original circuit.
Equivalent circuit for ideal transformer (reflecting secondary to primary):
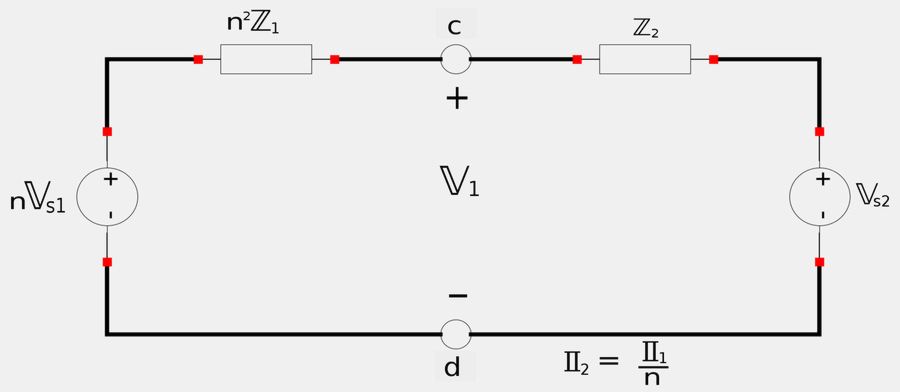
Reflecting primary to secondary
If we wanted to determine an equivalent circuit with the primary reflected to the secondary we would use a similar approach as above and obtain the following:
Rules for ideal transformer equivalent circuits
Reflecting secondary side to primary side
$$ 1) \; Divide \; secondary \; impedance \; by \; n^2 $$ $$ 2) \; Divide \; secondary \; voltage \; by \; n $$ $$ 3) \; multiply \; secondary \; current \; by \; n $$
Reflecting primary side to secondary side
$$ 1) \; Multiply \; primary \; impedance \; by \; n^2 $$ $$ 2) \; Multiply \; primary \; voltage \; by \; n $$ $$ 3) \; Divide \; primary \; current \; by \; n $$
Now let's take a look at some example problems involving ideal transformers.
Continue on to ideal transformers (example problem #1)...
