For the following circuit, determine the power absorbed by the 2 ohm resistor:
All values are RMS
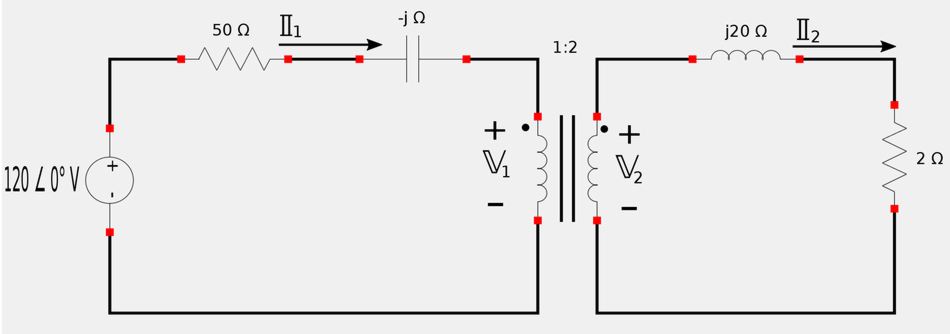
1) Apply Kirchhoff's Voltage Law (KVL) to primary side:
$$ \mathbb{I}_1(50-j)+\mathbb{V}_1=120 $$ $$ 50.01 \mathbb{I}_1 \angle 358.9^{\circ} + \mathbb{V}_1 = 120 \qquad , (Eqn\;1)$$ But by way of the turns ratio we know that: $$ \qquad \frac{\mathbb{V}_2}{\mathbb{V}_1} = \frac{N_2}{N_1} = n $$ $$ \qquad \frac{\mathbb{V}_2}{\mathbb{V}_1} = \frac{2}{1} $$ $$ \qquad \mathbb{V}_1 = \frac{\mathbb{V}_2}{2} $$ This means that we can write equation #1 as: $$ 50.01 \mathbb{I}_1 \angle 358.9^{\circ} + \frac{\mathbb{V}_2}{2} = 120 \qquad,(Eqn\;A)$$
2) Apply Kirchhoff's Voltage Law (KVL) to secondary side:
$$ \mathbb{I}_2(2+j20)-\mathbb{V}_2 = 0 \qquad(Eqn\;2) $$ Once again, by way of the turns ratio we know that: $$ \qquad \frac{\mathbb{I}_2}{\mathbb{I}_1} = \frac{N_1}{N_2} = \frac{1}{n} $$ $$ \qquad \frac{\mathbb{I}_2}{\mathbb{I}_1} = \frac{1}{2} $$ $$ \qquad \mathbb{I}_2 = \frac{\mathbb{I}_1}{2} $$ This allows us to rewrite equation #2 as: $$ \frac{\mathbb{I}_1}{2}(2+j20)-\mathbb{V}_2 = 0 $$ $$ 10.05 \mathbb{I}_1 \angle 84.29^{\circ} - \mathbb{V}_2 = 0 \qquad,(Eqn\;B) $$
3) Solve equations A and B:
We will solve equations A and B using Cramer's Rule. Start by putting the system of equations in matrix form: $$ \begin{pmatrix} 50.01 \angle 358.9^{\circ}&0.5&120\\ 10.05 \angle 84.29^{\circ}&-1&0\\ \end{pmatrix} $$ $$ D = \begin{vmatrix} 50.01 \angle 358.9^{\circ}&0.5\\ 10.05 \angle 84.29^{\circ}&-1\\ \end{vmatrix} = 50.65 \angle 184.6^{\circ} $$ $$ D_{\mathbb{I}_1} = \begin{vmatrix} 120&0.5\\ 0&-1\\ \end{vmatrix} = -120 $$ $$ \mathbb{I}_1 = \frac{D_{\mathbb{I}_1}}{D} = \frac{-120}{50.65 \angle 184.6^{\circ}} $$ $$ \mathbb{I}_1 = 2.37 \angle 355.4^{\circ} \; A $$ Above, we used the turns ratio to express I2 as: $$ \mathbb{I}_2 = \frac{\mathbb{I}_1}{2} $$ Therefore: $$ \mathbb{I}_2 = \frac{1}{2}(2.37 \angle 355.4^{\circ}) $$ $$ \mathbb{I}_2 = 1.185 \angle 355.4^{\circ} \; A $$
4) Determine power through resistor:
Noting that I2 is an RMS value and using our expressions for complex power, we can express the power through the 2 ohm resistor as: $$ \mathbb{S}_{2\Omega} = I^2 \mathbb{Z} $$ Since the load we are measuring is purely resistive, the complex power is also the real power. $$ \mathbb{S}_{2\Omega} = (1.185)^2 (2) = P_{2\Omega}$$
$$ P_{2\Omega} = 2.81 \; W $$
Let's look at another example problem involving ideal transformers.
Continue on to ideal transformers (example problem #2)...
