Determine Vo for the differential amplifier shown:
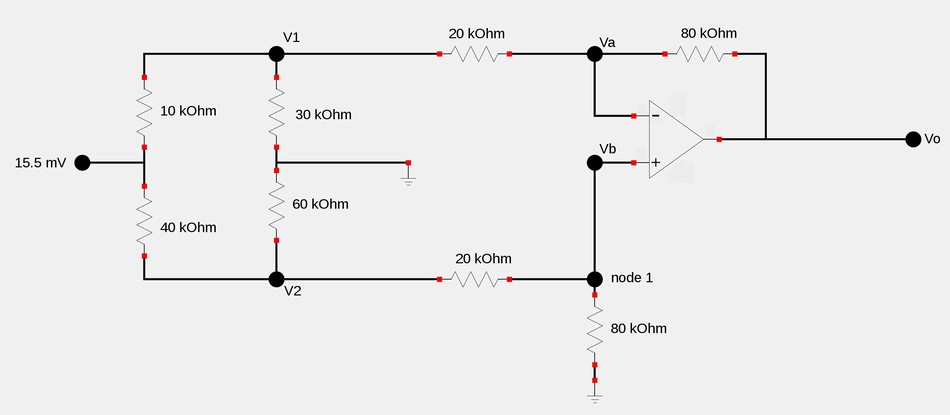
First let's determine values for V1 and V2. Applying Kirchoff's Current Law (KCL) at node V1 gives us: $$\frac{V_1-15.5 mV}{10,000} + \frac{V_1}{30,000} + \frac{V_1-V_a}{20,000} = 0 $$ $$\frac{V_1}{10,000} - (1.55 \times 10^{-6})+ \frac{V_1}{30,000} + \frac{V_1}{20,000} - \frac{V_a}{20,000}= 0 $$ $$\frac{11 V_1}{60,000} - \frac{V_a}{20,000} = 1.55 \times 10^{-6}$$
$$ \frac{11}{6}V_1 - \frac{1}{2}V_a = \frac{31}{2,000} \qquad,(Eqn \; 1)$$
Applying KCL at node V2 gives us: $$ \frac{V_2-15.5 mV}{40,000} + \frac{V_2}{60,000} + \frac{V_2}{100,000} = 0 $$ $$ \frac{V_2}{40,000} - (387.5 \times 10^{-9})+ \frac{V_2}{60,000} + \frac{V_2}{100,000} = 0 $$ $$ \frac{31}{600,000}V_2 = 387.5 \times 10^{-9} $$
$$V_2 = 7.5 \; mV$$
Next we apply KCL at node 1: $$\frac{V_b - V_2}{20,000} + \frac{V_b}{80,000} = 0$$ $$ \frac{V_b}{20,000} + \frac{V_b}{80,000} - \frac{V_2}{20,000} = 0 $$ $$ \frac{V_b}{16,000} = \frac{V_2}{20,000} $$ $$ V_b = \frac{4}{5}V_2 $$ Substituting our above-determined value for V2 gives us: $$ V_b = \frac{4}{5}(7.5 \times 10^{-3}) $$ $$ V_b = 6 \; mV $$ ...and by the 1st rule of ideal op-amps, Va must equal Vb, therefor:
$$ V_a = V_b = 6 \; mV $$
Substituting this value for Va into equation #1 from above gives us: $$ \frac{11}{6}V_1 - \frac{1}{2}(6 \; mV) = \frac{31}{2,000} $$
$$V_1 = 10.09 \; mV$$
Now that we have known values for V1 and V2 we recognize that our circuit resembles the one found in the Introduction to Differential Op-Amps page. Also, note that when comparing the circuit in this example to the template circuit used in the introduction page: $$\frac{R_1}{R_2} = \frac{R_3}{R_4} $$ ...must be true for the circuit to be a differential amplifier (which it is). Recalling our definition for the output of a differential amplifier: $$ V_o = \frac{R_2}{R_1}(V_2-V_1) $$ ...we substitute our values for this circuit: $$ V_o = \frac{80,000}{20,000}(7.5 \; mV - 10.09 \; mV) $$ ...which gives us a final answer of:
$$V_o = -10.36 \; mV$$
