For the following circuit, determine Vo in terms of V1 and V2:
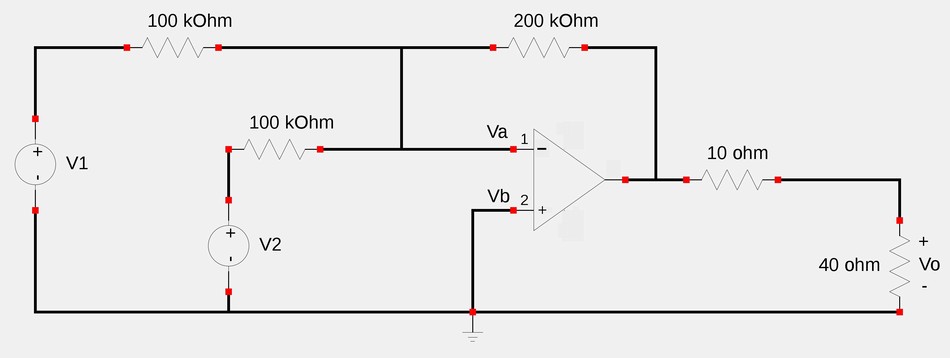
We will start by determining the output voltage of the summing op-amp (designated as "V3"). Start by recalling the definition of output voltage of a summing amplifier: $$ V_3 = - \Big[\frac{R_f}{R_1}V_1 + \frac{R_f}{R_2}V_2 \Big] $$ $$ V_3 = - \Big[\frac{200}{100}V_1 + \frac{200}{100}V_2 \Big]$$ $$ V_3 = - [2V_1 + 2V_2]$$ $$ V_3 = -2V_1 - 2V_2$$
$$ V_3 = -2V_1 - 2V_2$$
Now that we know the output voltage of the op-amp in terms of V1 and V2 (designated as "V3"), consider loop #1 of the circuit as depicted below (with symbolic mesh current "i").
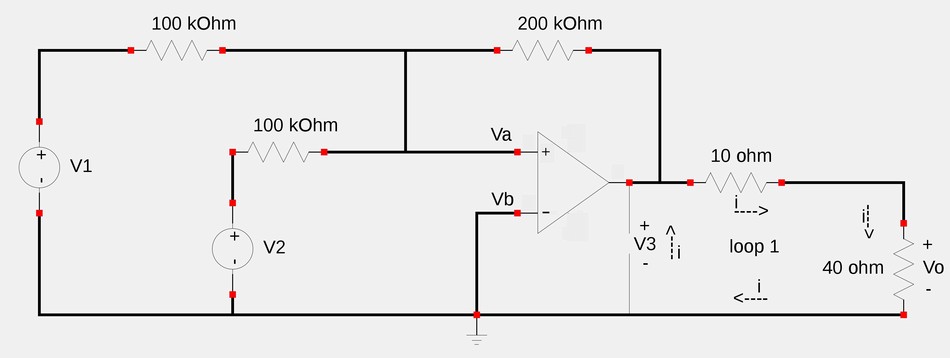
Applying Kirchoff's Voltage Law (KVL) around loop 1 in the direction of symbolic mesh current "i" gives us:
$$ 10i + 40i - [-2V_1 - 2V_2] = 0$$ $$ 10i + 40i + 2V_1 + 2V_2 = 0$$ $$ 50i = -2V_1 - 2V_2$$
$$ i = \frac{-V_1}{25} - \frac{-V_2}{25}$$
Finally, we recognize that we can use Ohm's Law to find Vo: $$ V_o = 40i $$ $$ V_o = 40 \Big[\frac{-V_1}{25} - \frac{-V_2}{25} \Big]$$
$$ V_o = -1.6V_1 - 1.6V_2 $$
