Differential amplifiers (also called difference amplifiers) are used when there is a need to amplify the difference between two input signals but reject any signal that are common to the two inputs. Consider the amplifier circuit shown below:
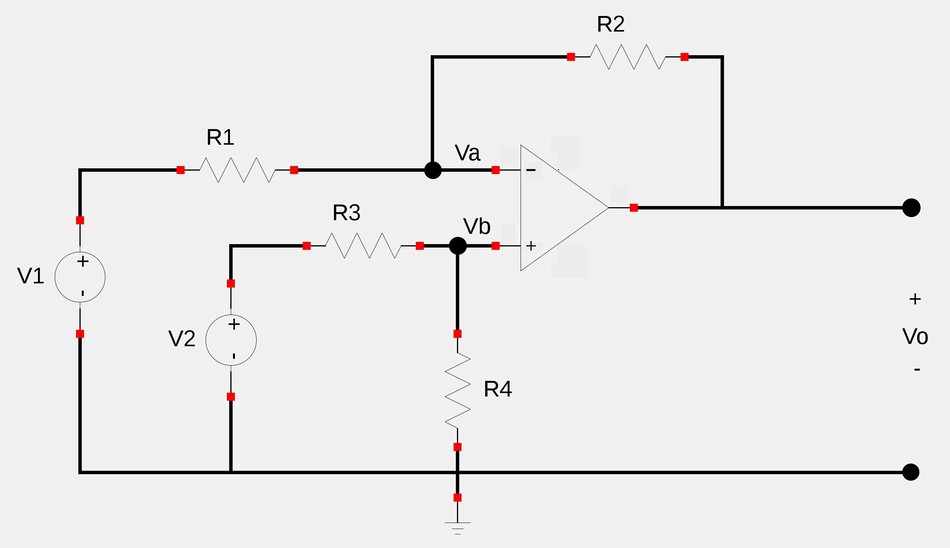
Applying Kirchoff's Current Law (KCL) at node "a" gives us: $$ \frac{V_1-V_a}{R_1} = \frac{V_a-V_o}{R_2} $$ $$ V_o = \Big( \frac{R_2}{R_1} + 1 \Big)V_a - \frac{R_2}{R_1}V_1 \qquad,(Eqn \; 1)$$
Applying KCL at node "b" gives us: $$ \frac{V_2-V_b}{R_3} = \frac{V_b}{R_4} $$ $$ V_b = \Big( \frac{R_4}{R_3+R_4} \Big) V_2 $$ ...and by the 1st rule of ideal op-amps we recall that Va=Vb, therefore: $$ V_a = \Big( \frac{R_4}{R_3+R_4} \Big) V_2 \qquad,(Eqn \; 2)$$
Substituting equation #2 into equation #1 gives us: $$V_o = \Big( \frac{R_2}{R_1} + 1 \Big) \Big( \frac{R_4}{R_3+R_4} \Big)V_2 - \frac{R_2}{R_1}V_1$$
$$V_o = \Bigg[ \frac{R_2 \Big( 1+\frac{R_1}{R_2} \Big)}{R_1 \Big( 1+\frac{R_3}{R_4} \Big)} \Bigg] V_2 - \Big( \frac{R_2}{R_1} \Big) V_1 \qquad,(Eqn \; 3)$$
In order for a differential amplifier to reject a signal common to the two inputs, it must have the following property: $$ V_o = 0 \; when \; V_1 = V_2$$ By examining equation #3, you can determine that such a property exists when: $$ \frac{R_1}{R_2} = \frac{R_3}{R_4} $$ ...which gives us an output value of:
$$V_o = \frac{R_2}{R_1}(V_2 - V_1)\qquad(Eqn \; 4 \; ,output \; of \; differential \; amplifier)$$
Subtractor:
Interestingly enough, when: $$ R_2=R_1 \; and \; R_3=R_4 $$ ...equation #4 becomes:
$$V_o = V_2-V_1 \qquad ,Subtractor$$
Let's take a look at an example:
Continue on to Differential Amplifier (example 1)
