Determine the value of Vo in the following circuit:
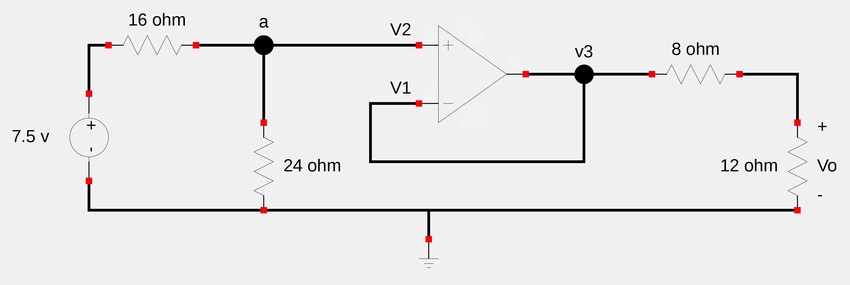
Recall our definition for the output voltage of a non-inverting op-amp (and note that in this schematic, the output voltage is v3, not Vo) $$V_3 = V_i \Big[ 1 + \frac{R_f}{R_1} \Big] \qquad(Eqn \; 1)$$ ,where Vi is the voltage applied to the non-inverting terminal, Rf is the feedback resistance between the output pin and the inverting terminal, and R1 is the resistance between ground and the inverting terminal. Since there is no feedback resistor (Rf=0) we can determine that: $$\frac{R_f}{R_1} = 0 $$ In order to first solve for the op-amp out put voltage (V3) we need to find the voltage on the non-inverting terminal (V2 in this case). Using Kirchoff's Current Law (KCL) at node a (and remembering that no current flows into the input terminals of an op-amp), we get:
$$\frac{7.5-V_a}{16} = \frac{V_a}{24} $$ Solving for Va gives us: $$V_a = 4.5 $$ and we note that : $$V_a = V_2 = V_i = 4.5 $$
We can now solve equation #1: $$V_3 = 4.5[1+0] $$ $$V_3 = 4.5 $$
With V3 now known, we can look at the circuit in the following manner:
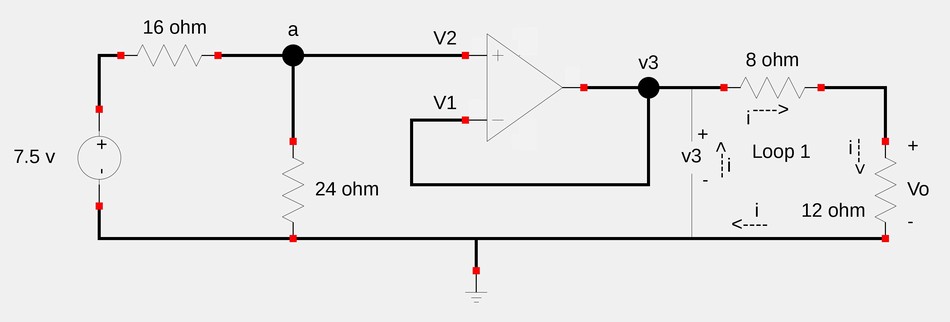
Applying Kirchoff's Voltage Law (KVL) around loop #1 in the direction of current (i): $$8i + 12i - V_3 = 0 $$ $$20i - 4.5 = 0 $$ $$i = 225 \; mA $$ Using Ohm's Law, we can now solve for Vo: $$V_o = 12i $$ $$V_o = 12(225 \times 10^{-3}) $$
$$V_o = 2.7 \;V $$
Let's take a look at another example.
Continue on to Non-inverting Op-Amps (example 2)...
