Determine the op-amp output current (io) for the following circuit:
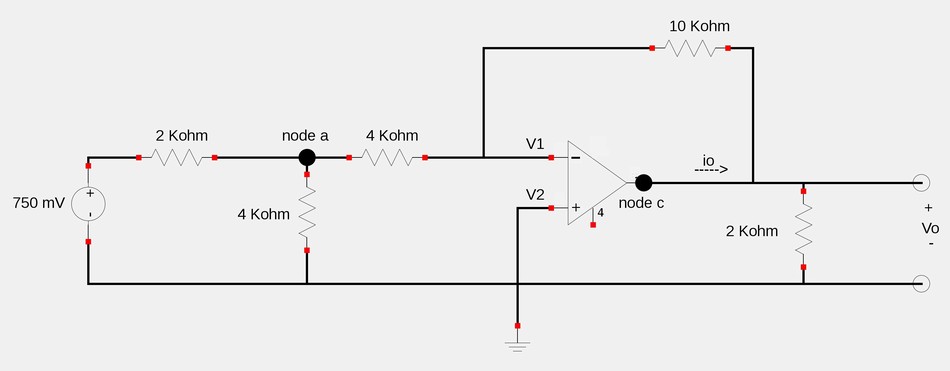
We will start by determining the output voltage of the amplifier (vo) and then use Kirchoff's Current Law (KCL) to determine io. Recall the definition of output voltage for an inverting amplifier: $$V_o = \frac{-R_f}{Ri}V_i \qquad(Eqn \; 1) $$ By examining the given circuit and comparing it to the circuit which we used to derive equation #1 in the Introduction to Inverting Op-Amps tutorial, we observe that Vi in this example is the voltage at node "a". The feedback resistor (Rf) is the 10k resistor and the input resistor (Ri) is the 4k resistor. Since we have all of those numerical values with the exception of Vi, we will proceed to determine the voltage at node "a". Using KCL at node #1 we get:
$$\frac{750mV - V_a}{2000} = \frac{V_a}{4000} + \frac{V_a - V_1}{4000}$$ Now recall the first rule of ideal op-amps which states that the V1=V2. Since V2 is grounded (equal to zero), then V1 must also be zero. We now have: $$\frac{750mV - V_a}{2000} = \frac{V_a}{4000} + \frac{V_a}{4000}$$ $$\frac{750mV - V_a}{2000} = \frac{2V_a}{4000}$$ $$\frac{750mV - V_a}{2000} = \frac{V_a}{2000} $$ $$(375 \times 10^{-6}) - \frac{V_a}{2000} = \frac{V_a}{2000} $$ $$\frac{2V_a}{2000} = (375 \times 10^{-6})$$ $$V_a = 0.375V $$ Substituting Va for Vi in equation #1 gives us: $$ V_o = \frac{-10000}{4000}(0.375) $$ $$V_o = -0.9375V $$
In order to solve for the output current of the op-amp (io), we will use KCL at node C: $$i_o = \frac{V_o-V_1}{10000} + \frac{V_o}{2000} $$ Recall that V1=0: $$i_o = \frac{V_o}{10000} + \frac{V_o}{2000} $$ $$i_o = \frac{-0.9375}{10000} + \frac{-0.9375}{2000} $$
$$i_o = -562.5 \mu A $$
Let's take a look at another example
Continue on to Inverting Op-Amps (example 2)...
