For the following circuit, Calculate Vo if Vs=2V:
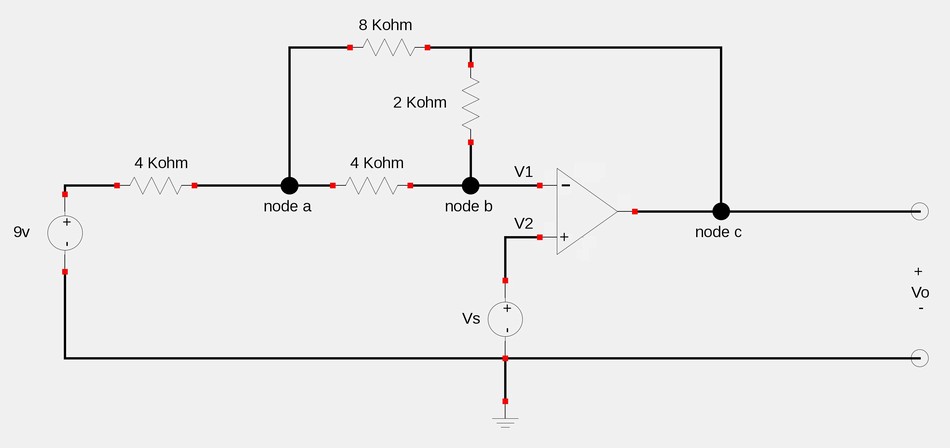
This problem is a little trickier with the multiple power supplies and arrangement of resistors that doesn't allow us to readily apply our derived formula for the output voltage of an inverting op-amp. In fact, from what we have learned so far, it's not easy to tell if this is an inverting op-amp at all. Nevertheless, we can still use our 2 rules for ideal op-amps as well as Kirchoff's Current Law (KCL) to solve the problem
Start by realizing that if Vs=2, the V2=2. By the first law of ideal op-amps: $$V_1=V_2 $$ ...which means that: $$V_1=2v = the \; voltage \; at \; node \; b$$
Since it appears that we have two unknowns (Va and Vo) in our circuit, we will attemp to get two separate equations that we can solve. Start by applying KCL at node a: $$\frac{9-V_a}{4000} = \frac{V_a-V_b}{4000} + \frac{V_a-V_o}{8000} $$ $$9-V_a = V_a - V_b + \frac{V_a}{2} - \frac{V_o}{2} \qquad,where \; V_b=2$$ $$-V_a - \frac{V_a}{2} -V_a + \frac{V_o}{2} = -2-9$$ $$5V_a - V_o = 22 \qquad(Eqn \; 1) $$
Now apply KCL at node b: $$\frac{V_a-V_b}{4000} = \frac{V_b-V_o}{2000} \qquad,where \; V_b=2$$ $$\frac{V_a}{4000} - \frac{2}{4000} = \frac{2}{2000} - \frac{V_o}{2000} $$ $$V_a + 2V_o = 6 \qquad(Eqn \; 2) $$ If we go ahead and solve the system of two equations with two unknowns (equations 1 and 2), we determine that: $$V_a = 4.54 V $$ as well as:
$$V_o=727.27 mV $$
