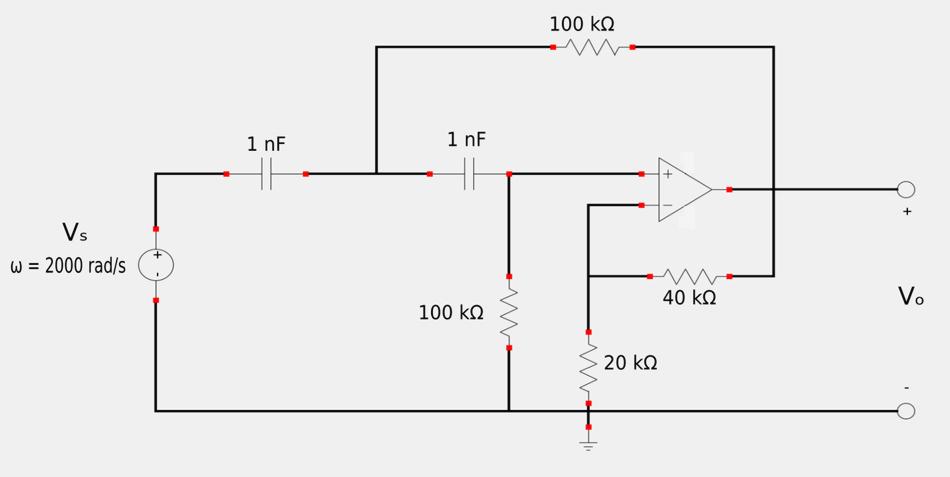
Determine the closed-loop gain and phase-shift of the output voltage with respect to input voltage
As usual, we begin by converting the circuit from the time-domain to the frequency/phasor domain (with labeled nodes and nodal voltage representations):
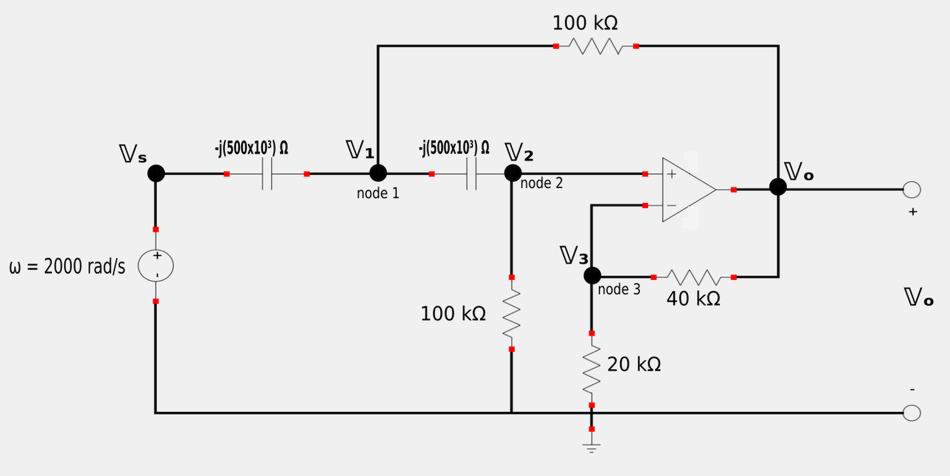
Apply Kirchhoff's Current Law (KCL) to node #1:
$$ \frac{\mathbb{V}_1-\mathbb{V}_s}{-j(500\times 10^3)} + \frac{\mathbb{V}_1-\mathbb{V}_o}{100\times 10^3} + \frac{\mathbb{V}_1-\mathbb{V}_2}{-j(500\times 10^3)} = 0 $$ Multiplying the above expression by 500,000 gives us: $$ j\mathbb{V}_1 - j\mathbb{V}_s + 5\mathbb{V}_1 - 5\mathbb{V}_o + j\mathbb{V}_1 - j\mathbb{V}_2 = 0 $$ $$ -5\mathbb{V}_o + \mathbb{V}_1(5+j2) -j\mathbb{V}_2 - j\mathbb{V}_s = 0$$ Converting the above epression to polar form gives us:
$$ -5\mathbb{V}_o + 5.385\mathbb{V}_1 \angle 21.8^{\circ} + \mathbb{V}_2 \angle (-90^{\circ}) + \mathbb{V}_s \angle (-90^{\circ}) = 0 \qquad,(I) $$
Apply (KCL) to node #3:
$$ \frac{\mathbb{V}_3}{20,000} + \frac{\mathbb{V}_3-\mathbb{V}_o}{40,000} = 0 $$ Multiplying the above expression by 40,000 gives us: $$ 2\mathbb{V}_3 + \mathbb{V}_3 - \mathbb{V}_o = 0 $$ $$ 3\mathbb{V}_3 = \mathbb{V}_o $$
$$ \mathbb{V}_3 = \frac{\mathbb{V}_0}{3} \qquad,(II) $$
Apply (KCL) to node #2:
$$ \frac{\mathbb{V}_2-\mathbb{V}_1}{-j(500\times 10^3)} + \frac{\mathbb{V}_2}{100\times 10^3} = 0 $$ Multiplying the above expression by 500,000 gives us: $$ j\mathbb{V}_2 - j \mathbb{V}_1 + 5\mathbb{V}_2 = 0 $$ $$ -j\mathbb{V}_1 + \mathbb{V}_2(5+j) = 0 $$ After converting the above expression to polar form we get:
$$ \mathbb{V}_1 \angle (-90^{\circ}) + 5.099\mathbb{V}_2 \angle 11.31^{\circ} = 0 \qquad,(III) $$
Using the rules for ideal op-amps:
We know that the following must be true: $$ \mathbb{V}_2 = \mathbb{V}_3 $$ ...and since we already have an expression for V3 (see equation II above), we obtain the following:
$$ \mathbb{V}_2 = \mathbb{V}_3 = \frac{\mathbb{V}_0}{3} \qquad,(IV) $$
Substitute equation (IV) into equation (III):
$$ \mathbb{V}_1\angle (-90^{\circ}) + 5.099 \Big( \frac{\mathbb{V}_o}{3} \Big) \angle 11.31^{\circ} = 0 $$ $$ \mathbb{V}_1\angle (-90^{\circ}) + 1.7\mathbb{V}_o \angle 11.31^{\circ} = 0 $$ $$ \mathbb{V}_1\angle (-90^{\circ}) = -1.7\mathbb{V}_o \angle 11.31^{\circ} $$ $$ \mathbb{V}_1 = \frac{-1.7\mathbb{V}_o \angle 11.31^{\circ}}{1\angle(-90^{\circ})} $$ $$ \mathbb{V}_1 = -1.7\mathbb{V}_o\angle101.3^{\circ} $$
$$ \mathbb{V}_1 = 1.7\mathbb{V}_o \angle 281.3^{\circ} \qquad,(V) $$
Substitute equations (V) and (IV) into equation (I):
$$ -5\mathbb{V}_o + (5.385\angle21.8^{\circ})(1.7\mathbb{V}_o \angle 281.3^{\circ}) + \Big( \frac{\mathbb{V}_o}{3} \Big)(1\angle(-90^{\circ}) + \mathbb{V}_s \angle(-90^{\circ}) = 0 $$ $$ -5\mathbb{V}_o + 9.155\mathbb{V}_o\angle 303.1^{\circ} + 0.3333\mathbb{V}_o\angle(-90^{\circ}) + \mathbb{V}_s \angle (-90^{\circ}) = 0 $$ $$ 8.033\mathbb{V}_o \angle(-90^{\circ}) = -\mathbb{V}_s\angle (-90^{\circ}) = \mathbb{V}_s \angle 90^{\circ} $$ $$ \frac{8.033\mathbb{V}_o}{\mathbb{V}_s} \angle (-90^{\circ}) = 1 \angle 90^{\circ}$$ $$ \frac{\mathbb{V}_o}{\mathbb{V}_s} = \frac{1\angle 90^{\circ}}{8.033 \angle (-90^{\circ})} $$ After evaluating the above expression, we arrive at our gain and phase-shift: $$ \frac{\mathbb{V}_o}{\mathbb{V}_s} = 0.1245 \angle 180^{\circ} $$
The above expression represents a gain of 0.1245 and a positive phase-shift of 180 degrees (in terms of the output voltage with respect to input voltage).
Let's take a look at one final example:
Continue on to AC op-amp circuits example 3
