For the following circuit: A) Determine the oscillator frequency, B)Determine the minimum value of "R" for which oscillations will be sustained:
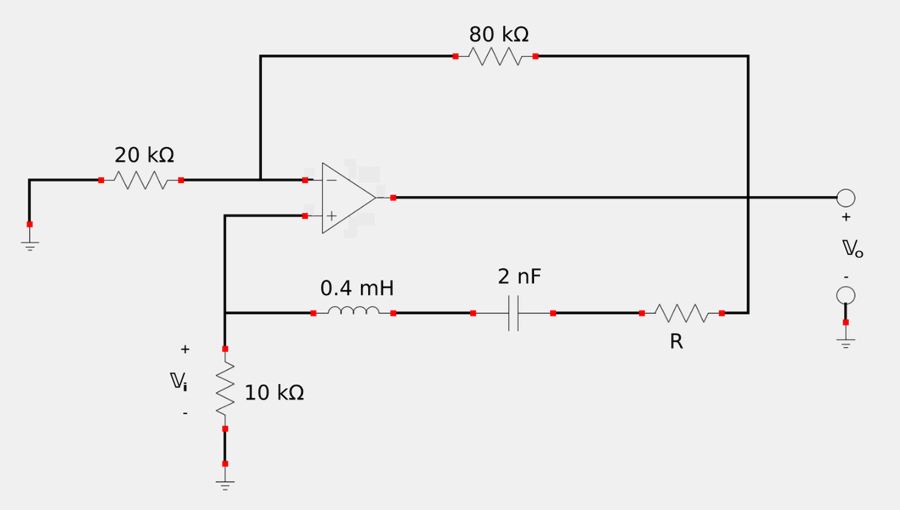
Part A
Recall the second Barkhausen criterion, which states that the overall phase-shift (from input to output) must be zero. This means that Vi and Vo must be in phase. Start by defining the feedback ratio as: $$ feedback \; ratio = \frac{\mathbb{V}_i}{\mathbb{V}_o} $$ which when expressed in terms of impedances is: $$ = \frac{10,000}{R+10,000 + j\omega(0.4\times10^{-3}) - \frac{j}{\omega(2\times10^{-9})}} $$ $$ \frac{\mathbb{V}_i}{\mathbb{V}_o} = \frac{10,000}{R+10,000 + j \Big(\omega(0.4\times10^{-3}) - \frac{1}{\omega(2\times10^{-9})} \Big) } $$ In order for there to be no phase shift, the above expression must be completely real meaning that the "j" component must equal zero. To better understand this, examine the following graph of the complex plane:
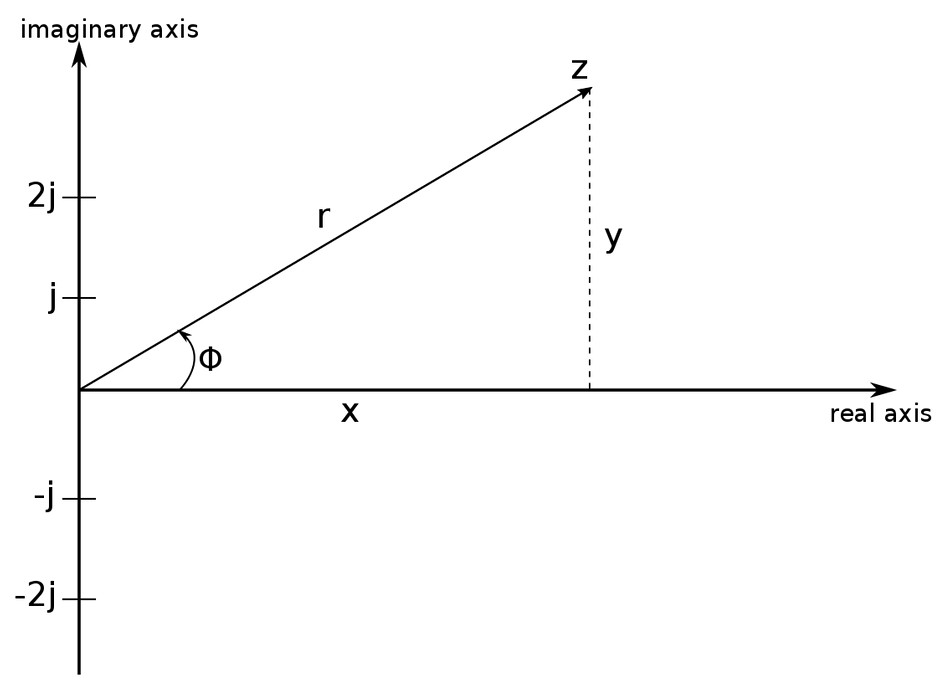
Note that as long as there is any "j" component, the number is not completely real and a phase angle will exist. Therefore, equating the "j" component of the above expression to zero gives us: $$ \omega(0.4\times10^{-3}) - \frac{1}{\omega(2\times10^{-9})} = 0 $$ $$ \omega(0.4\times10^{-3}) = \frac{1}{\omega(2\times10^{-9})} $$ $$ \omega^2 (800\times 10^{-15}) = 1 $$ $$ \omega^2 = 1.25\times 10^{12} $$ $$ \omega = (1.118\times 10^6) \frac{radians}{second} $$ Recall that : $$ \omega = 2\pi f $$ $$ f = \frac{\omega}{2\pi} = \frac{1.118\times 10^6}{2\pi}$$ $$ f = (177.9 \times 10^3) \; Hz $$
$$ f = 177.9 \; kHz = oscillator \; frequency $$
Part B
Express the gain of the op-amp in terms of Vo/Vi using the non-inverting input: $$ Gain = \frac{\mathbb{V}_o}{\mathbb{V}_i} $$ $$ \frac{\mathbb{V}_o}{\mathbb{V}_i} = \frac{R+10,000 + j \Big(\omega(0.4\times10^{-3}) - \frac{1}{\omega(2\times10^{-9})} \Big)}{10,000} $$ In part "A" we determined that omega is: $$ \omega = (1.118\times 10^6) $$ ...and we also know that when omega is equal to this value, the "j" component is equal to zero, therefore our expression for gain now becomes: $$ \frac{\mathbb{V}_o}{\mathbb{V}_i} = \frac{R+10,000}{10,000} \qquad,(Eqn \; 1) $$
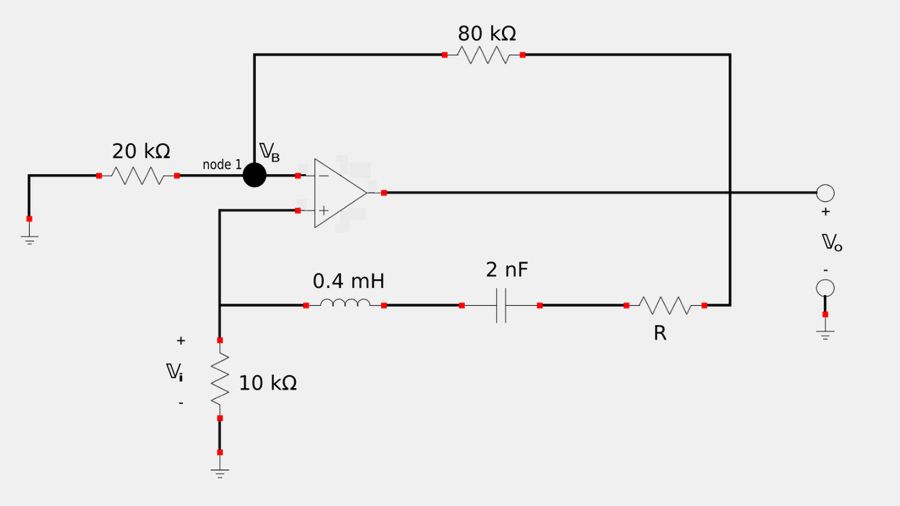
Now we apply Kirchhoff's Current Law (KCL) at node 1 and derive an expression for the gain of the op-amp using the inverting input: $$ \frac{\mathbb{V}_B}{20,000} + \frac{\mathbb{V}_B - \mathbb{V}_o}{80,000} = 0 $$ Multiplying the above expression by 80,000 gives us: $$ 4\mathbb{V}_B + \mathbb{V}_B - \mathbb{V}_o = 0 $$ $$ 5\mathbb{V}_B = \mathbb{V}_o $$ $$ \frac{\mathbb{V}_o}{\mathbb{V}_B} = 5 $$ However, by the rules for ideal op-amps we know that: $$ \mathbb{V}_B = \mathbb{V}_i $$ Therefore: $$ \frac{\mathbb{V}_o}{\mathbb{V}_i} = 5 \qquad, (Eqn \; 2) $$ This represents the minimum gain needed to sustain oscillations. With this in mind we now substitute equation 2 into equation 1: $$ 5 \leq \frac{R+10,000}{10,000} $$ $$ 50,000 \leq R+10,000 $$
$$ R \geq 40 k\Omega $$ Hence, R must be at least 40 kOhm in order for the circuit to sustain oscillations.
