Determine Vo for the following circuit.
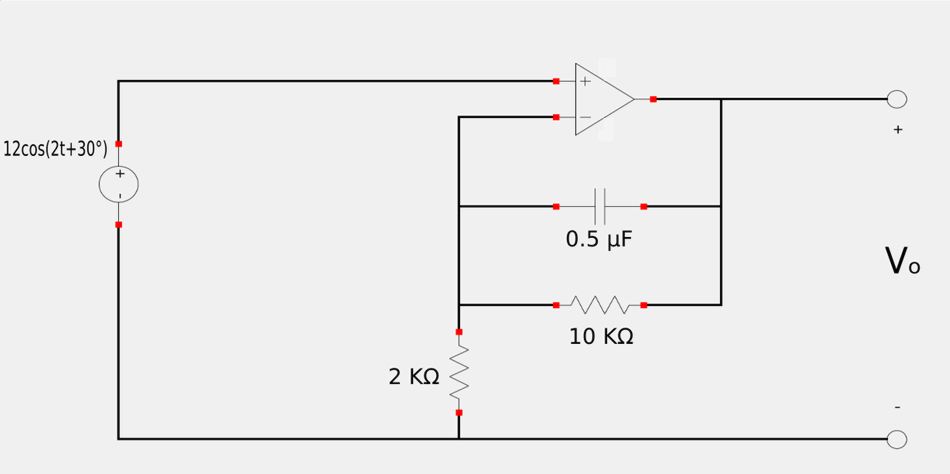
From the introduction to non-inverting DC amplifiers page, we can readily see that the op-amp in the above circuit is in a non-inverting configuration. Recall that for a non-inverting amplifier driven by a DC source, the output voltage is defined by: $$V_o = V_i \Big( 1+\frac{R_f}{R_1} \Big)$$ The concept for a non-inverting amplifier driven by an AC source is the same except we replace resistances with impedances and deal with complex numbers in the phasor domain. Therefore we determine the output phasor voltage using the following expression: $$ \mathbb{V}_o = \mathbb{V}_i \Big( 1+\frac{\mathbb{Z}_f}{\mathbb{Z}_1} \Big) \qquad,Expression \; 1$$
Start by transforming the given circuit to the phasor domain:
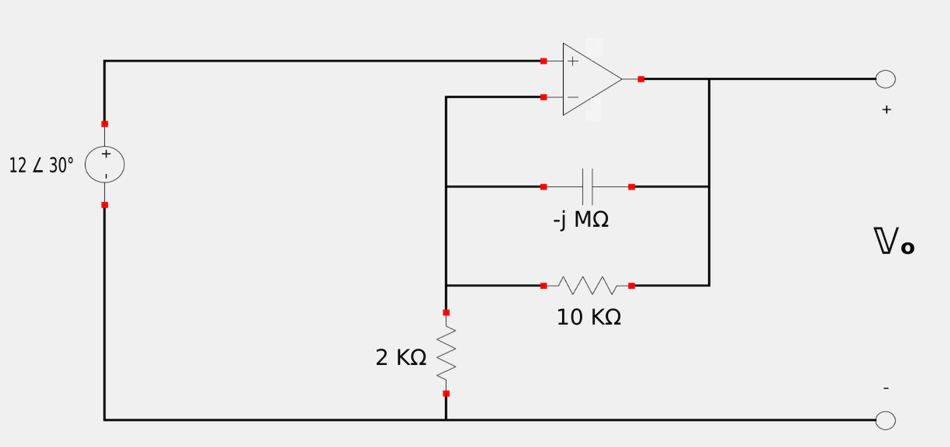
Our feedback impedance is the following parallel combination: $$ \mathbb{Z}_f = -j \; M\Omega || 10 \; K\Omega$$ $$ = \frac{1}{\frac{1}{-j\;M\Omega}+\frac{1}{10,000}} $$ $$ = \frac{1}{(j \times 10^{-6}) + (100 \times 10^{-6})} $$ $$ = \frac{1}{(100\times 10^{-6})\angle0.5729^{\circ}} $$ $$ \mathbb{Z}_f = 10,000 \angle (-0.5729^{\circ}) $$
By simple inspection we see that: $$ \mathbb{Z}_1 = 2,000 $$
We now substitute our values into expression #1: $$ \mathbb{V}_o = 12\angle 30^{\circ} \Big[ 1 + \frac{10,000\angle(-0.5729^{\circ})}{2,000} \Big] $$ $$ = 12\angle 30^{\circ} [6\angle(-0.4774^{\circ})] $$ $$ \mathbb{V}_o = 72\angle 29.52^{\circ} = 72e^{j29.52^{\circ}} $$
To convert the phasor output voltage to the time domain, we multiply by e^jwt and take the real part of the result: $$ V_o = R_e \{ 72e^{j29.52^{\circ}} e^{j2t} \} $$ $$ = R_e \{ 72e^{j(2t+29.52^{\circ})} \} \qquad,Eqn \; 2$$
Recall Euhler's Identity: $$ e^{j\theta} = \cos\theta + j\sin\theta $$ ...and apply it to equation #2:
$$ V_o = R_e \{ 72\cos(2t+29.52^{\circ}) + j72\sin(2t+29.52^{\circ}) \} $$
$$ V_o = 72\cos(2t+29.52^{\circ}) $$
Next we will learn how to determine the gain and phase-shift of an AC op-amp circuit without knowing the amplitude of the input voltage:
Continue on to AC op-amp circuits example 2
