For the following circuit, determine Vo and Io (leave answer in phasor form)
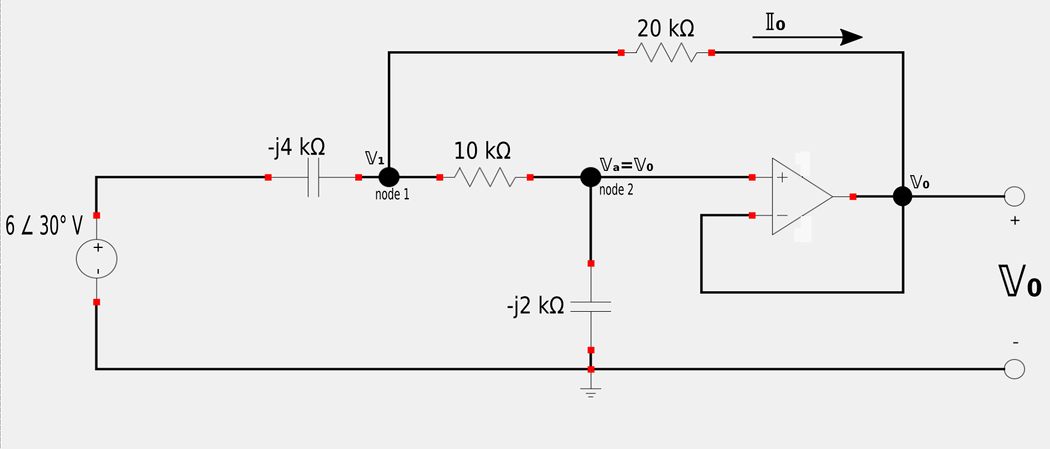
You will notice that the circuit is already displayed in the phasor/frequency domain. Also, by the rules for an ideal op-amp, the inverting and non-inverting input voltages must be equal. Since the inverting input is tied to Vo, then we know that the non-inverting input (Va) must also be equal to Vo. (Hence the label Va=Vo in the circuit schematic found at node 2.)
Apply Kirchoff's Current Law (KCL) at node 1:
$$ \frac{\mathbb{V}_1-6\angle 30^{\circ}}{-j4,000} + \frac{\mathbb{V}_1-\mathbb{V}_o}{10,000} + \frac{\mathbb{V}_1-\mathbb{V}_o}{20,000} = 0 $$ Multiplying the above expression by 20,000 gives us: $$ j5\mathbb{V}_1 - j30\angle 30^{\circ} + 2\mathbb{V}_1 - 2\mathbb{V}_o + \mathbb{V}_1 - \mathbb{V}_o = 0 $$ $$ j5\mathbb{V}_1 + \Big[30\angle(-90^{\circ})\Big]\Big[1\angle 30^{\circ}\Big] + 2\mathbb{V}_1 - 2\mathbb{V}_o + \mathbb{V}_1 - \mathbb{V}_o = 0 $$ $$ j5\mathbb{V}_1 + 30\angle (-60^{\circ}) + 2\mathbb{V}_1 - 2\mathbb{V}_o + \mathbb{V}_1 - \mathbb{V}_o = 0 $$ $$ -3\mathbb{V}_o + \mathbb{V}_1(3+j5) = -30\angle (-60^{\circ}) $$
$$ -3\mathbb{V}_o + 5.831\mathbb{V}_1 \angle 59.04^{\circ} = 30\angle 120^{\circ} \qquad,(I) $$
Apply Kirchoff's Current Law (KCL) at node 2:
$$ \frac{\mathbb{V}_o-\mathbb{V}_1}{10,000} + \frac{\mathbb{V}_o}{-j2,000} = 0 $$ Multiplying the above expression by 10,000 gives us: $$ \mathbb{V}_o - \mathbb{V}_1 + j5\mathbb{V}_o = 0$$ $$ \mathbb{V}_o(1+j5) - \mathbb{V}_1 = 0 $$ $$ 5.1\mathbb{V}_o \angle 78.69^{\circ} - \mathbb{V}_1 = 0 $$
$$ \mathbb{V}_1 = 5.1\mathbb{V}_o \angle 78.69^{\circ} \qquad,(II) $$
Substitute equation (II) into equation (I):
$$ -3\mathbb{V}_o + \Big( 5.831\angle 59.04^{\circ} \Big)\Big( 5.1\mathbb{V}_o \angle 78.69^{\circ} \Big) = 30\angle 120^{\circ} $$ $$ -3\mathbb{V}_o + 29.74\mathbb{V}_o \angle 137.7^{\circ} = 30\angle 120^{\circ} $$ $$ 32.02\mathbb{V}_o \angle 141.3^{\circ} = 30\angle 120^{\circ} $$
$$ \mathbb{V}_o = 0.9369 \angle (-21.3^{\circ}) \qquad,Final \; answer \; for \; \mathbb{V}_o $$
Determine Io:
By examining the circuit and noting the direction of current flow for Io we see that: $$ \mathbb{I}_o = \frac{\mathbb{V}_1-\mathbb{V}_o}{20,000} $$ Substitute equation (II) into the above expression: $$ \mathbb{I}_o = \frac{5.1\mathbb{V}_o\angle 78.69^{\circ} - \mathbb{V}_o}{20,000} $$ $$ = \frac{5.001\mathbb{V}_o\angle 90^{\circ}}{20,000} $$ Substitute our recently determined value for Vo into the above expression: $$ \mathbb{I}_o = \frac{\Big[ 5.001\angle90^{\circ} \Big] \Big[0.9369\angle (-21.3^{\circ}) \Big]}{20,000} $$ $$ = \frac{4.685 \angle 68.7^{\circ}}{20,000} $$
$$ \mathbb{I}_o = (234.3 \angle 68.7^{\circ}) \mu A \qquad,Final \; answer \; for \; \mathbb{I}_o$$
We shall now look at a couple of applications of op-amp circuits, starting with capacitance multipliers:
Continue on to capacitance multiplying circuit...
