A capacitance multiplier circuit is constructed with op-amps and is used to produce a multiple of a small physical capacitance. The circuit will resemble the one shown below:
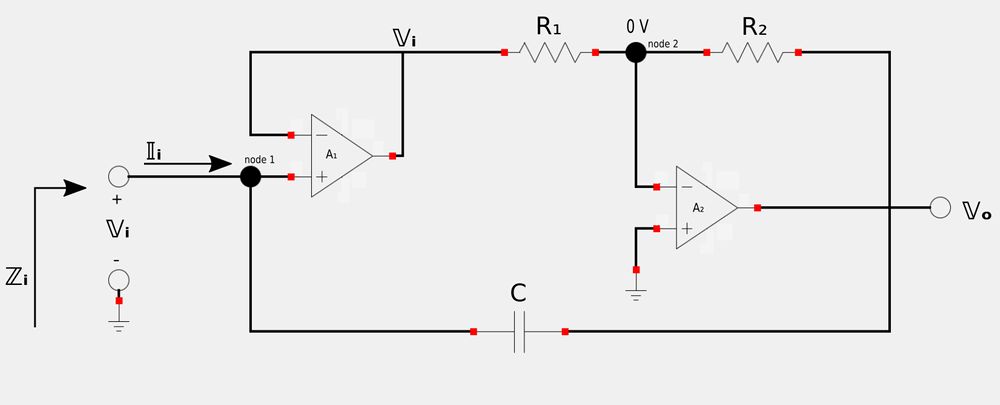
In the above schematic the 1st op-amp (A1) acts as a voltage follower which isolates any capacitance generated by the circuit from the loading created the the second op-amp (A2). Op-amp A2 is an inverting amplifier.
Recall from the rules of ideal op-amps (Found in the introduction to op-amps tutorial) that no current flows into the input terminals of an op-amp and that the voltages present on the two input terminals must be equal. For the above circuit, these two rules for ideal op-amps allow us to determine the output voltage of A1 as being Vi and the node 2 voltage as being equal to zero.
If we apply Kirchhoff's Current Law (KCL) to node 1 of the above circuit, we get:
$$ \mathbb{I}_1 = \frac{\mathbb{V}_i - \mathbb{V}_o}{\frac{1}{j\omega C}} $$
$$ \mathbb{I}_i = j\omega C(\mathbb{V}_i-\mathbb{V}_o) \qquad,(eqn \; I) $$
If we apply KCL to node 2 we get:
$$ \frac{0-\mathbb{V}_i}{R_1} + \frac{0-\mathbb{V}_o}{R_2} = 0 $$ $$ \frac{-\mathbb{V}_o}{R_2} = \frac{\mathbb{V}_i}{R_1} $$
$$ \mathbb{V}_o = \frac{-\mathbb{V}_i (R_2)}{R_1} \qquad.(eqn \; II) $$
Substitute eqn II into eqn I:
$$ \mathbb{I}_i = j\omega C \Big(\mathbb{V}_i + \frac{\mathbb{V}_i R_2}{R_1} \Big) $$ $$ \mathbb{I}_i = j\omega C \mathbb{V}_i \Big(1 + \frac{R_2}{R_1} \Big) $$ $$ \frac{\mathbb{I}_i}{\mathbb{V}_i} = j\omega \Big( 1 + \frac{R_2}{R_1} \Big) C $$ let: $$ \qquad C_{eq} = \Big( 1 + \frac{R_2}{R_1} \Big) C $$ therefore: $$ \frac{\mathbb{I}_i}{\mathbb{V}_i} = j\omega C_{eq} $$
We know know that: $$ input \; impedance = \mathbb{Z}_i = \frac{\mathbb{V}_i}{\mathbb{I}_i} = \frac{1}{j \omega C_{eq}} $$ ...where: $$ \qquad C_{eq} = \Big( 1 + \frac{R_2}{R_1} \Big) C $$
By selecting suitable values for R1 and R2, the circuit can be made to produce a capacitance between the input terminal and ground (which is a multiple of "C")
However, the size of C_eq is constrained by the limits of the inverted output voltage of amplifier A2
The larger the capacitance multiplier value, the smaller the allowable input voltage can be before the op-amp becomes saturated.
Example:
Determine the equivalent capacitance of the following circuit:
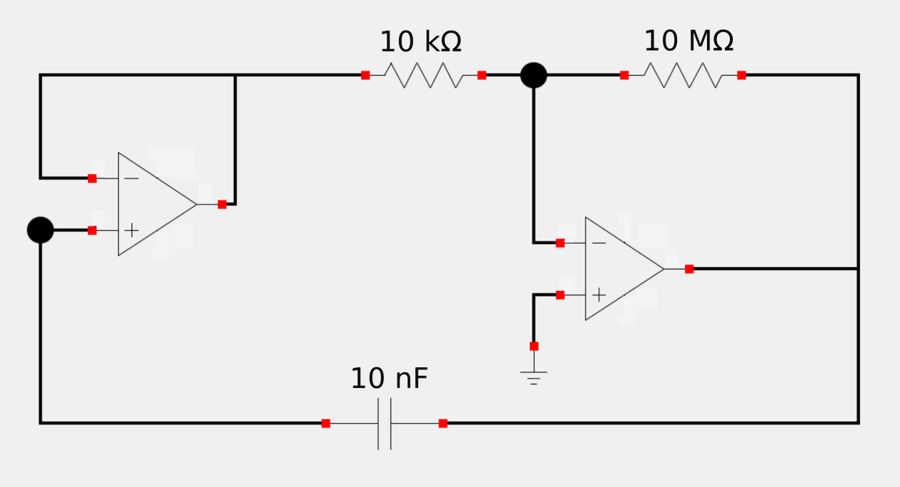
$$ \qquad C_{eq} = \Big( 1 + \frac{R_2}{R_1} \Big) C $$ $$ C_{eq} = \Big( 1 + \frac{10 \times 10^6}{10 \times 10^3} \Big) (10 \times 10^{-9}) $$
$$ C_{eq} = 10.01 \mu F $$
Lastly, we will look at a final application of op-amps where we learn how they can be used as oscillators:
Continue on to op-amp oscillators...
